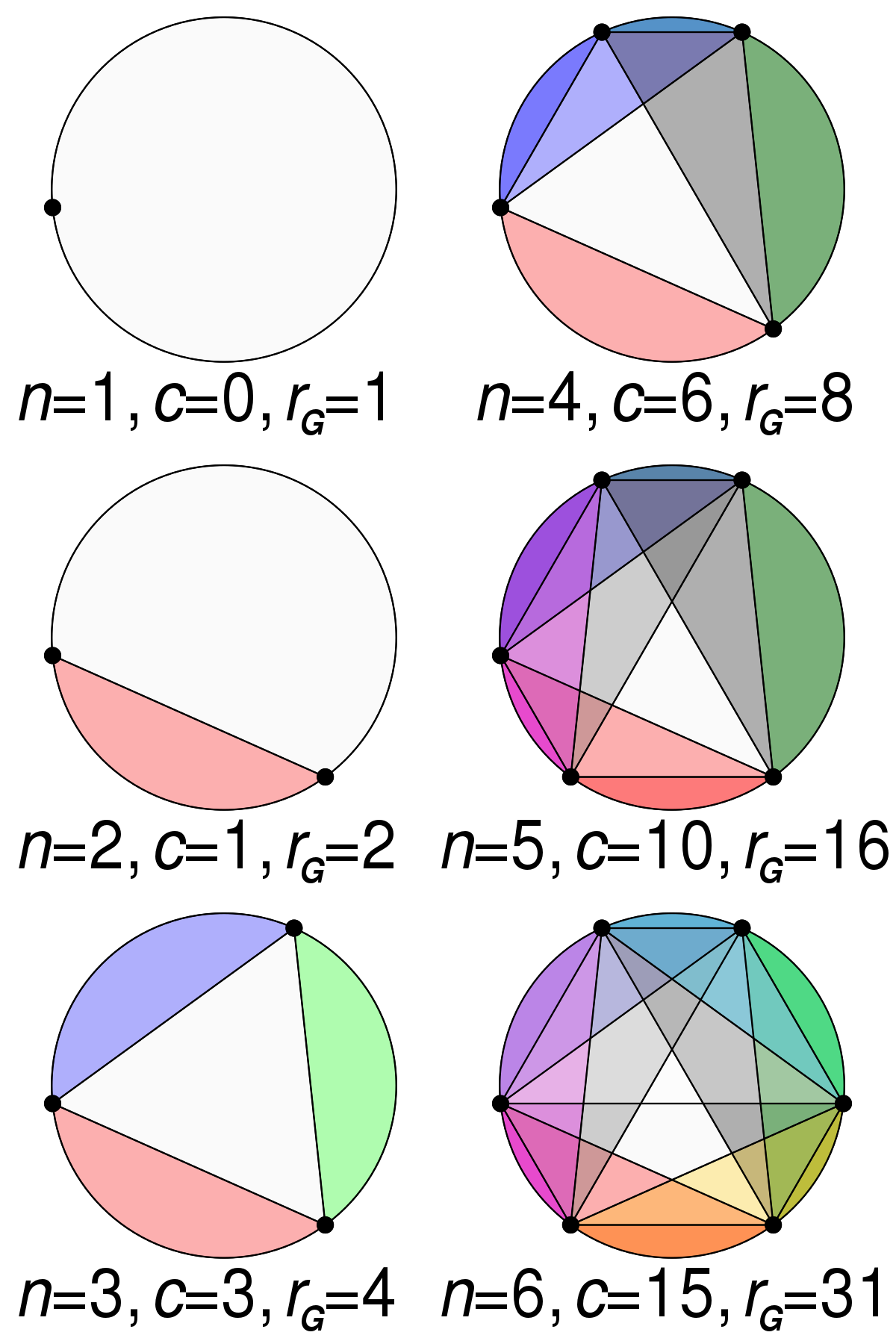
1, 2, 4, 8, 16, 31

跳转到导航跳转以在几何中搜索，借助于与n侧面的铭刻多边形将圆圈分成区域的问题，以最大化边缘和对角线创造的区域的数量，有时称为Moser＆＃39; S圆圈问题，具有归纳方法的解决方案。最大可能数量的区域，r g =（n 4）+（n 2）+ 1，给出序列1,2,4,8,16,31,57,99,163,256，......（OEIS ：A000127）。虽然前五个术语匹配几何进度2 n - 1，但它在n = 6时发散，显示出在少数观察中揭开的风险。

如果圆上存在n个点并添加一个点，则可以从新点绘制n行到以前存在的点。两种情况也是可能的。在第一种情况下（a）中，新行通过了两个或多个旧行（在先前存在的点之间）交叉的点。在第二种情况（b）中，新线在不同的点中交叉每条旧行。了解以下事实将是有用的。

引理。可以选择新的点A，以便为每个新行发生情况。

证明。对于案例A，三个点必须在一行：新的点A，绘制线的旧点O，以及两个旧行相交的点i。有n个旧点o，因此有限很多点我，其中两个旧线路相交。对于每个o和i，线路oi在O的一点中穿过圆圈。由于圆圈具有无限的点，因此它具有一个点，这不会是线路OI。然后，对于这一点A和所有旧点O，案例B将是真的。

这种引理意味着，如果有k线路交叉AO，则它们中的每一个在不同点交叉AO，并且由线AO创建K + 1个新区域。

雷姆玛建立了解决问题的重要财产。通过采用感应证据，可以在F（N - 1）方面到达F（n）的公式。

在图中，暗线是将点1到4连接到8个总区域（即f（4）= 8）。该图示出了用虚线从n = 4到n = 5的诱导步骤。当添加第五点时（即，当使用F（4）计算F（5））时，这导致添加四条新线（图中的虚线），编号为1到4，每个点为单位连接到。因此，由第五点引入的新区域的数量可以通过考虑由4行中的每一个添加的区域的数量来确定。设置i计算正在添加的线条。每个新行都可以跨越许多现有行，具体取决于它到的点（i的值）。除了新的点之外，新行永远不会互相交叉。

可以通过考虑＆＃34上的点数来确定每个新线相交的线数;左＆＃34;线条和＆＃34的点数;右和＃34;这条线。由于所有现有点都有它们之间存在线，因此左侧的点数乘以右侧的点数是将跨越新行的行数。对于指出的线，我有

在此示例中，向i = 1和i = 4的行每个横向零线，而行到i = 2并且i = 3每个交叉两行（在一侧有零点，另一个侧面）。

f（n）= f（n - 1）+σi= 1 n - 1（1 +（n - i-1）（i-1））{\ displaystyle f（n）= f（n-1）+ \ sum _ {i = 1} ^ {n-1} \ left（left（ni-1 \右）\左（i-1 \右）\右）}

f（n）= f（n - 1）+σi= 1 n - 1（2 - n + ni - i 2）{\ displaystyle f（n）= f（n-1）+ \ sum _ {i =左（2-n + ni-i ^ {2} \右）}左（2-n + ni-i ^ {2}）}

使用第一（n - 1）{\ displaystyle（n-1）}自然数和第一个（n - 1）{\ displaystyle（n-1）}正方形的总和，这组合到

f（n）= f（n - 1）+ 1 6 n 3 - n 2 + 17 6 n - 2 {\ displaystyle f（n）= f（n-1）+ {\ frac {1} {6}} n ^ {3} -n ^ {2} + {\ frac {17} {6}} n-2}

f（n）=σk= 1 n（1 6 k 3 - k 2 + 17 6 k-2）+ 1 {\ displaystyle f（n）= \ sum _ {k = 1} ^ {n} \ left（ {\ frac {1} {6}} k ^ {3} -k ^ {2} + {\ frac {17} {6}} k-2 \右）+1}用f（0）= 1 {\ DISPLAYSTYLE F（0）= 1}

f（n）= n 24（n 3 - 6 n 2 + 23 n-18）+ 1 {\ displaystyle f（n）= {\ frac {n} {24}}（n ^ {3} -6n ^ { 2} + 23n-18）+1}

lemma断言，如果全部＆＃34;内部＆＃34;和弦的交叉点很简单（正是两个和弦穿过内部的每个交叉点）。如果圆上的点被选中＆＃34，这将是这种情况;一般位置＆＃34;在这个假设＆＃34;泛型交叉点＆＃34;，区域数量也可以以非归纳方式确定，使用连接的平面图的欧拉特征的公式（这里被视为嵌入在其中的图形2-球形S 2）。

平面图确定具有F面（二维单元），E边缘（1维小区）和V顶点（0维小区）的平面的单元分解。当图表连接时，2维球体S 2的欧拉关系

持有。以上面的图形（所有和弦）视图（圆圈）作为平面图。如果可以找到V和E的一般公式，则也可以推导出F的公式，这将解决问题。

其顶点包括圆上的n点，称为外部顶点，以及内部顶点，圆形内部的不同和弦的交叉点。 ＆＃34;通用交叉点＆＃34;上面提出的假设保证了每个内部顶点是不超过两个和弦的交叉点。

因此，确定V中的主要任务是找到内部顶点的数量。由于引理的后果，任何两个交叉的和弦都会唯一地确定内部顶点。这些和弦依次由和弦的四个相应的端点确定，这些端点都是外部顶点。任何四个外部顶点都决定了循环四边形，并且所有循环四边形都是凸四边形，因此每组四个外部顶点具有由其对角线（和弦）形成的一点交叉点。此外，通过定义通过交叉和弦形成所有内部顶点。

因此，每个内部顶点由四个外部顶点的组合唯一确定，其中内部顶点的数量由

v = v外部+ v内部= n +（n 4）。 {\ displaystyle v = v _ {\ text {exterior}} + v _ {\ text {interile}} = n + {n \选择4}。}

边缘包括连接相邻的外部顶点的对的n圆弧，以及通过集合的集合在圆内部创建的十字线段（下面描述）。由于有两组顶点：外部和内部，可以进一步分类为三组：

直接边缘（未被其他和弦切割）连接两个外部顶点。这些是相邻的外部顶点之间的和弦，并形成多边形的周边。有n这样的边缘。

要查找组2和3中的边的数量，请考虑每个内部顶点，该内部顶点连接到恰好四个边。这种收益率为

边缘。由于每个边缘由两个端点顶点定义，因此仅列举内部顶点，因此仅计数组2边缘的组2边缘仅计算一次。

由另一个（即，第1组的和第1组的和弦）切割的每个和弦必须包含两个第3组边缘，其开始和结束的曲线细分。由于和弦由两个外部顶点独特地确定，因此有一共

第3组边缘。这是两倍于本身不是第1组成员的人数的总数。

这些结果的总和除以两个，给出了组2和3中的组合数。从第1组添加n边缘，n圆弧边缘带来总计

E = 4（n 4）+ 2（（n 2） - n）2 + n + n = 2（n 4）+（n 2）+ n。 {\ displaystyle e = {\ frac {4 {n \选择4} +2 \ left（{n \ choical 2} -n \ light）} {2}} + n + n = 2 {n \选择4} + {n \选择2} + n。}

将V和e代入为f，f = e-v + 2，{\ displaystyle \，f = e-v + 2，}一个求解的欧拉关系。然后获得一个

f =（n 4）+（n 2）+ 2. {\ displaystyle f = {n \选择4} + {n \选择2} +2。}

由于其中一个面是圆的外部，因此圆内部的区域r g的数量是f-1，或者

r g =（n 4）+（n 2）+ 1，{\ displaystyle r_ {g} = {n \选择4} + {n \选择2} +1，}

r g = n！ （n - 4）！ 4！ + n！ （n - 2）！ 2！ + 1 {\ displaystyle r_ {g} = {\ frac {n！} {（n-4）！4！}} + {\ frac {n！} {（n-2）！2！}} + 1}

r g = 1 24 n（n 3 - 6 n 2 + 23 n - 18）+ 1 {\ displaystyle r_ {g} = {\ frac {1} {24} n（n ^ {3} -6n ^ { 2} + 23n-18）+1} Conway，J. H.和Guy，R. K.＆＃34;有多少个地区。＆＃34; 在数字书中。 纽约：Springer-Verlag，PP。76-79,1996。