齐奥尔科夫斯基火箭方程

跳转到导航跳转搜索齐奥尔科夫斯基火箭方程、经典火箭方程或理想火箭方程是一个描述遵循火箭基本原理的飞行器运动的数学方程：通过高速驱逐部分质量来利用推力对自身施加加速度的装置，因此可以由于动量守恒而移动。

Δv=v e ln⁡m 0 m f=i sp g 0 ln⁡m 0 m f{\DisplayStyle\Delta v=v_{\Text{e}}\ln{\frac{m_{0}}{m_{f}=i_{\Text{sp}}g_{0}\ln{\frac{m_{0}}{m_{f}。

Δv{\DisplayStyle\Delta v\}是Δv-车辆速度的最大变化(没有外力作用)。

M0{\displaystyle m_{0}}是包括推进剂在内的初始总质量，也称为湿质量。

Mf{\displaystyle m_{f}}是不含推进剂的最终总质量，也称为干质量。

Ve=i sp g 0{\displaystyle v_{\text{e}}=i_{\text{sp}}g_{0}}是有效排气速度，其中：

这个方程式是以俄罗斯科学家康斯坦丁·齐奥尔科夫斯基(俄语：КонстантинЦиолковский)的名字命名的，他独立推导了这个方程式，并在他1903年的工作中发表了它。[1]这个方程式早在1810年由英国数学家威廉·摩尔(William Moore)[2]推导出来，后来在1813年出版了另一本书。[3]威廉·利奇部长是一位有能力的科学家，他也在1861年独立得出了火箭学的基本原理。

虽然火箭方程式的推导是一项直截了当的微积分练习，但齐奥尔科夫斯基被誉为第一个将其应用于火箭是否能达到太空旅行所需速度的问题。

美国的罗伯特·戈达德在1912年独立开发了这个方程式，当时他开始研究如何改进火箭发动机，以应对可能的太空飞行。欧洲的赫尔曼·奥伯斯(Hermann Oberth)在研究太空旅行的可行性时，大约在1920年独立推导出了这个方程式。

在下面的推导中，火箭被认为是指火箭及其所有未燃烧的推进剂。

牛顿第二运动定律将外力(Fi{\Displaystyle F_{i}，})与整个系统(包括火箭和排气)的线性动量的变化联系起来，如下所示：

∑F i=LIMΔt→0 P 2−P 1Δt{\DisplayStyle\SUM F_{i}=\LIM_{\DELTA t\TO 0}{\FRAC{P_{2}-P_{1}}{\DELTA t}。

其中P1{\displaystyle P_{1}\，}是火箭在时间t=0{\displaystyle t=0}时的动量：

P2{\DisplayStyle P_{2}\，}是火箭在时间t=Δt{\DisplayStyle t=\Deltat\，}时的动量和排气质量：

P2=m(V+ΔV)+Δm Ve{\DisplayStyle P_{2}=m\Left(V+\DeltaV\Right)+\Delta MV_{\Text{e}。

V{\displaystyle V\，}是火箭在时间t=0{\displaystyle t=0}时的速度

V+ΔV{\DisplayStyle V+\DeltaV\，}是火箭在时间t=Δt{\DisplayStyle t=\Deltat\，}的速度。

V e{\DisplayStyle V_{\Text{e}}\，}是在时间Δt{\DisplayStyle\Deltat\，}期间添加到排气(并被火箭损失)的质量的速度。

M+Δm{\DisplayStyle m+\Deltam\，}是火箭在时间t=0{\DisplayStyle t=0}时的质量。

M{\DisplayStyle m\，}是火箭在时间t=Δt{\DisplayStyle t=\Deltat\，}时的质量。

观察者框中排气Ve{\displaystyle V_{\text{e}的速度与火箭框ve{\displaystyle v_{\text{e}中的排气速度相关(因为排气速度为负方向)。

P2−P1=mΔV−v eΔm{\DisplayStyle P_{2}-P_{1}=m\Delta V-v_{\Text{e}}\Delta m\，}。

并且，使用dm=−Δ_m{\Δ_dm=-\deltam}，由于弹出正显示样式{\Display_Style\Δm}导致质量减小，

∑F i=m d V d t+v e d m d t{\DisplayStyle\SUM F_{i}=m{\frac{dv}{dt}}+v_{\text{e}}{\frac{dm}{dt}

如果没有外力，则∑F i=0{\DisplayStyle\SUM F_{i}=0}(线性动量守恒)和。

M d V d t=−v e d m d t{\DisplayStyle m{\frac{dv}{dt}}=-v_{\text{e}}{\frac{dm}{dt}。

∫V V+ΔV d V=−v e∫m 0 m 1 1m d m{\DisplayStyle\int_{V}^{V+\Delta V}\，\mathm{d}V={-v_{e}}\int_{m_{0}}^{m_{1}}{\frac{1}{m}}\，\mathrm{d}m}。

ΔV=v e ln⁡m 0 m 1{\DisplayStyle\Delta V=v_{\Text{e}}\ln{\frac{m_{0}}{m_{1}。

M 1=m 0 e−ΔV/v e{\DisplayStyle m_{1}=m_{0}e^{-\DeltaV\/v_{\Text{e}{0=m 0 e−ΔV/v e{\DisplayStyle m_{0}=m_{。1}e^{\DeltaV/v_{\Text{e}显示样式0−m 1=m 1(eΔV/v e−1){\DisplayStyle m_{0}-m_{1}=m_{1}\Left(e^{\Delta V/v_{\Text{e}-1\Right)}。

其中m0{\displaystyle m_{0}}是包括推进剂的初始总质量，m1{\displaystyle m_{1}}是最终总质量，v e{\displaystyle v_{\text{e}是火箭相对于火箭的排气速度(比冲，或者，如果按时间测量，则乘以地球重力加速度)。

值m 0−m 1{\DisplayStyle m_{0}-m_{1}}是所消耗的推进剂的总质量，因此：

M f=1−m 1 m 0=1−e−ΔV/v e{\DisplayStyle M_{f}=1-{\frac{m_{1}}{m_{0}=1-e^{-\DeltaV/v_{\Text{e}

其中Mf{\displaystyle M_{f}}是推进剂质量分数(用作工作质量的初始总质量的一部分)。

ΔV{\DisplayStyle\Delta V\，}(增量v)是使用火箭发动机产生的加速度大小随时间的积分(如果没有外力，实际加速度是多少)。在自由空间中，对于速度方向的加速度，这就是速度的增加。如果是相反方向的加速度(减速)，那就是速度的降低。当然，重力和阻力也会加速车辆，它们可以增加或减少车辆所经历的速度变化。因此，δ-v通常不是车辆速度或速度的实际变化。

该方程也可以从质量上力(推力)形式的加速度的基本积分中导出。通过将δ-v方程表示为以下表达式：

Δv=∫t 0 t 1|T|m 0−tΔm和d t{\DisplayStyle\Delta v=\int_{t0}^{t1}{\frac{|T|}{{m_{0}}-{t}\Delta{m}~dt}。

其中T是推力，m0{\DisplayStyle m_{0}}是初始(湿)质量，Δm{\DisplayStyle\Deltam}是初始质量减去最终(干)质量，

并且认识到合力随时间的积分是总冲量，假设推力是唯一涉及的力，

Jdln⁡(M 0)−ln⁡(M 1)Δm{\DisplayStyle J~{\FRAC{\ln({m_{0}})-\ln({m_{1}})}{\Delta m}}。

意识到质量变化上的冲量等于推进剂质量流率(P)上的力，推进剂质量流率(P)本身就等于排气速度，

JΔm=F p=V e x h{\displaystyle{\frac{J}{\Delta m}}={\frac{F}{p}}=V_{\rm{exh}。

Δv=V e x h和ln⁡(M 0 M 1){\DisplayStyle\Delta v=V_{\rm{exh}}~\ln\Left({\frac{m_{0}}{m_{1}\Right)}。

想象一下，一枚火箭静止在太空中，没有任何力施加在它身上(牛顿第一运动定律)。从发动机启动的那一刻起(时钟设置为0)，火箭以恒定的质量流速p(kg/s)和相对于火箭的排气速度v e(m/s)排出气体质量。这产生了一个恒定的力来推动火箭，等于p×ve。火箭最初携带的燃料质量等于m0-mf。质量流率被定义为火箭在燃烧时间内的总湿质量，因此燃烧所有这些燃料需要等于(m0-mf)/p的时间。火箭受到恒定的力(M×Ve)，但它的总重量正在稳步下降，因为它正在排出气体。根据牛顿第二运动定律，它在任何时刻的加速度等于它的推进力除以它当前的质量：

A=d v dt=−v e ln⁡(m o−(m o−m f))+v e ln⁡(m 0−0)=v e ln⁡(M 0)−v e ln⁡(m f。)⁡(M 0 M F)。{\DisplayStyle~a={\Frac{dv}{dt}}=~-v_{\text{e}}\ln(m_{o}-(m_{o}-m_{f}))+v_{\text{e}}\ln(m_{0}-0)=~v_{\text{e}}\ln(m_{0})-v_{\text{e}}\ln(m_{f})~=~v_{\text{e}}\ln\Left({。\frac{m_{0}}{m_{f}\右)。}。

如果考虑到狭义相对论，可以推导出相对论火箭的下列方程[4]，其中Δv{\DisplayStyle\Δv}再次表示火箭'；火箭在静止开始的惯性参照系中的最终速度(在排出其所有反应质量并减少到静止质量m1{\displaystyle m_{1}}之后)(包括燃料的静止质量最初为m0{\displaystyle m_{0}})，c{\displaystyle c}表示真空中的光速：

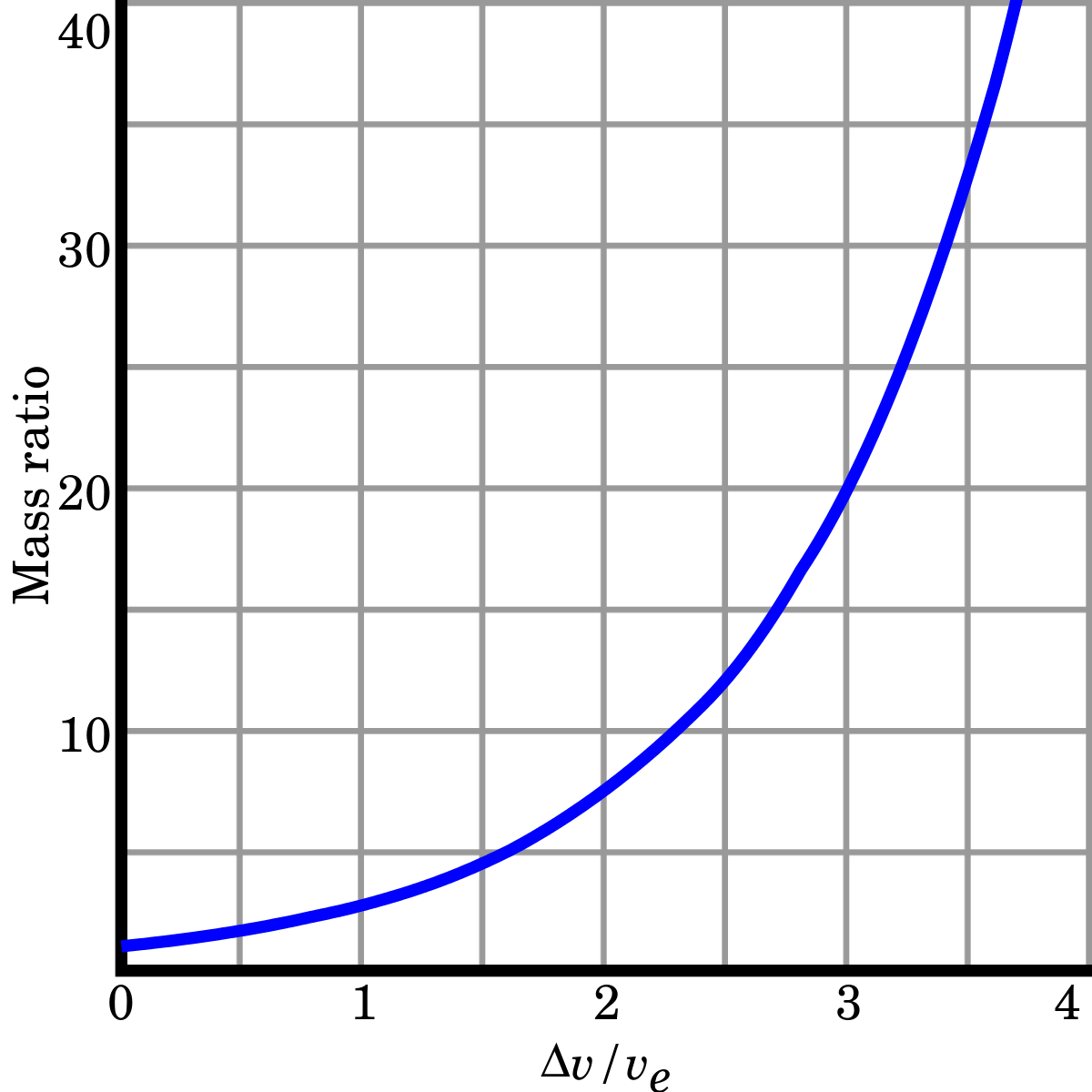
M 0 m 1=[1+Δv c 1−Δv c]c 2v e{\displaystyle{\frac{m_{0}}{m_{1}=\left[{\frac{1+{\frac{\Delta v}{c}{1-{\frac{\Delta v}{c}。}\右]^{\frac{c}{2v_{\text{e}。

将m 0 m 1{\displaystyle{\frac{m_{0}}{m_{1}写为R{\displaystyle R}允许将此公式重新排列为。

Δv c=R2 v e c−1 R 2 v e c+1{\DisplayStyle{\frac{\Delta v}{c}}={\frac{R^{\frac{2v_{\text{e}{c}}-1}{R^{\frac{2v_{\text{e}{c}}+1}}

然后，使用单位R2 v e c=exp⁡[2v e c ln⁡R]{\displayStyle R^{\frac{2v_{\text{e}{c}}=\exp\Left[{\frac{2v_{\text{e}{c}}\ln R\right]}(这里"；exp"；表示指数函数；另请参阅自然对数以及对数恒等式的幂等式)和恒等式tanh⁡x=e 2 x−1 e 2x+1{\displaystyle\tanh x={\frac{e^{2x}-1}{e^{2x}+1}}(参见双曲函数)。

Δv=c tanh⁡(v e c ln⁡m 0 m 1){\DisplayStyle\Delta v=c\tanh\Left({\frac{v_{\text{e}{c}}\ln{\frac{m_{0}}{m_{1}\right)}。

Δv(字面意思是速度变化)，象征为Δv，发音为Delta-vee，用于航天器飞行动力学，是执行诸如从行星或月球发射或着陆，或太空轨道机动所需的冲量。它是以速度为单位的标量。在此上下文中使用的，它与车辆速度的物理变化不同。

Δ-v是由反应发动机(如火箭发动机)产生的，与单位质量的推力和燃烧时间成正比，用于通过火箭方程式确定给定机动所需的推进剂质量。

对于行星际任务，δ-v通常绘制在猪排图上，该图显示了作为发射日期函数的所需任务Delta-v。

在航空航天工程中，推进剂质量分数是运载器质量中没有到达目的地的部分，通常用来衡量运载器的性能。换句话说，推进剂质量分数是推进剂质量与车辆初始质量之间的比率。在航天器中，目的地通常是轨道，而对于飞机来说，它是它们的着陆位置。质量分数越高，表示设计中的重量越轻。另一个相关的度量是有效载荷分数，它是有效载荷初始重量的分数。

有效排气速度通常被指定为比冲量，它们通过以下方式相互关联：

Ve{\displaystyle v_{\text{e}}是以m/s为单位测量的比冲，与以m/s为单位测量的有效排气速度相同(如果g为ft/s 2，则为ft/s)。

G 0{\DisplayStyle g_{0}}是标准重力，9.80665米/秒2(使用英制单位32.174米/秒2)。

火箭方程将火箭飞行物理的要点集中在一个简短的方程中。当有效排气速度恒定时，它也适用于类似火箭的反作用飞行器；当有效排气速度变化时，它可以求和或积分。火箭方程式只考虑火箭发动机的反作用力，不包括可能作用在火箭上的其他力，如空气动力或重力。因此，当使用它来计算从有大气层的行星发射(或动力下降到)的推进剂需求时，这些力的影响必须包括在Delta-V需求中(见下面的例子)。在所谓的火箭等式的暴政中，火箭可以携带的有效载荷是有限度的，因为更高的推进剂会增加整体重量，因此也会增加燃料消耗。[5]该公式不适用于非火箭系统，如空中拦截器、火炮发射、太空升降机、发射回路、系绳推进或光帆。

火箭方程式可以应用于轨道机动，以确定需要多少推进剂才能改变到特定的新轨道，或者由于特定的推进剂燃烧而找到新的轨道。当应用于轨道机动时，假设是脉冲机动，即推进剂被释放并瞬间施加δ-v。这一假设对于短期烧伤来说是相对准确的，比如中途校正和眼眶插入动作。随着燃烧持续时间的增加，由于在动作持续时间内重力对车辆的影响，结果的准确性会降低。对于小推力、长持续时间的推进，如电力推进，更复杂的分析是基于航天器状态矢量的传播和推力积分来预测轨道运动。

假设排气速度为4,500米/秒(15,000英尺/秒)，Δv{\DisplayStyle\Delta v}为9,700米/秒(32,000英尺/s)(地球到LEO，包括Δv{\DisplayStyle\Delta v}，以克服重力和空气动力阻力)。

单级入轨火箭：1−e−9.7/4.5{\displaystyle 1-e^{-9.7/4.5}}=0.884，因此初始总质量的88.4%必须是推进剂。剩下的11.6%用于发动机、油箱和有效载荷。

两级入轨：假设第一级应提供5,000米/秒(16,000英尺/秒)的Δv{\DisplayStyle\Delta v}；1−e−5.0/4.5{\DisplayStyle 1-e^{-5.0/4.5}}=0.671，因此初始总质量的67.1%必须是第一级的推进剂。剩余质量为32.9%。在第一级处理后，质量仍然等于这32.9%，减去第一级的坦克和发动机的质量。假设这是初始总质量的8%，那么还剩下24.9%。第二级应提供4,700米/秒(15,000英尺/秒)的Δv{\DisplayStyle\Delta v}；1−e−4.7/4.5{\displaystyle 1-e^{-4.7/4.5}}=0.648，因此剩余质量的64.8%必须是推进剂，这是原始总质量的16.2%，剩余的8.7%用于第二级的坦克和发动机、有效载荷，对于航天飞机，还包括轨道器。因此，所有发动机、坦克和有效载荷总共有16.7%的原始发射质量可用。

在顺序推进火箭级的情况下，该方程适用于每一级，其中对于每一级，方程中的初始质量是丢弃前一级后火箭的总质量，而方程中的最终质量是恰好在丢弃有关级之前的火箭的总质量。对于每个阶段，特定的冲量可能是不同的。

例如，如果火箭80%的质量是第一级的燃料，10%是第一级的干质量，10%是剩余的火箭，那么

Δv=v e ln⁡100 100−80=v e ln⁡5=1.61v e.。{\displaystyle{\BEGIN{ALIGNED}\Delta v\&；=v_{\text{e}}\ln{100\Over 100-80}\\&；=v_{\text{e}}\ln 5\\&；=1.61v_{\text{e}}。\end{aligned}。

对于每个阶段，有三个类似的、随后较小的阶段，具有相同的v e{\displaystyle v_{\text{e}，我们有。

Δv=3 v e lnΔ5⁡=4.83 v e{\DisplayStyle\Delta v\=3v_{\Text{e}}\ln 5\=4.83v_{\Text{e}}。

有效载荷为初始质量的10%×10%×10%=0.1%。

一枚可比的SSTO火箭，也有0.1%的有效载荷，燃料箱和发动机的质量可能是11.1%，燃料的质量可能是88.8%。这会给你。

Δv=v e ln⁡(100/11.2)x=2.19v e.。{\displaystyle\Delta v\=v_{\text{e}}\ln(100/11.2)\=2.19v_{\text{e}}。}。

如果在前一级被丢弃之前点燃新一级的发动机，并且同时工作的发动机具有不同的比冲(就像固体火箭助推器和液体燃料级经常出现的情况一样)，情况就会更加复杂。

当火箭被视为变质量系统时，不能直接用牛顿第二运动定律来分析，因为该定律只适用于等质量系统。[6][7][8]如果Tsiolkovsky火箭方程看起来类似于相对论性力方程F=dp/dt=mdv/dt+vdm/dt{\displaystyle F=dp/dt=m\；dv/dt+v\；dm/dt}，可能会引起混淆。用m(T){\displaystyle m(T)}作为火箭的变质量，似乎推导出了齐奥尔科夫斯基火箭方程，但这种推导是不正确的。请注意，有效排气速度v e{\displaystyle v_{\text{e}甚至没有出现在此公式中。

^К。Ціолковскій，Изслѣдованіемировыхъпространствъреактивнымиприборами，1903年(在这里可以在线获得，2011年8月15日在回程机器存档的稀疏的pdf)。

威廉·摩尔；伍尔维奇军事学院(1810年)。“自然哲学杂志”，C。

.