光镊子

跳转到导航跳转搜索光学镊子(最初称为单光束梯度力阱)是一种科学仪器，它使用高度聚焦的激光束来保持和移动微观物体，如原子、纳米颗粒和液滴，其方式与镊子类似。如果物体在没有额外支撑的情况下保持在空气或真空中，就可以称之为光学悬浮。

根据粒子和周围介质之间的相对折射率，激光提供吸引力或排斥力(通常约为皮牛顿量级)。如果光的力量抵消了重力，悬浮是可能的。捕获的颗粒通常是微米或更小的。电介质和吸收粒子也可以被捕获。

光学镊子被用于生物学和医学(例如，抓住和保持单个细菌或细胞，如精子细胞、血细胞或DNA)、纳米工程和纳米化学(研究和构建单分子材料)、量子光学和量子光力学(研究单个粒子与光的相互作用)。阿瑟·阿什金(Arthur Ashkin)对光学镊子的发展受到了2018年诺贝尔物理学奖的赞誉。

贝尔实验室的科学家亚瑟·阿什金于1970年首次报道了微米大小颗粒上的光学散射和梯度力的探测。[1]几年后，阿什金和他的同事们首次观察到了现在通常所说的光学镊子：一束紧密聚焦的光束，能够使微观粒子在三维空间保持稳定。[2]2018年，阿什金因这一进展被授予诺贝尔物理学奖。

1986年这篇开创性论文的作者之一朱(Steven Chu)继续在他的工作中使用光学镊子来冷却和囚禁中性原子。[3]这项研究为朱赢得了1997年的诺贝尔物理学奖，与克劳德·科恩-坦诺吉(Claude Cohen-Tannoudji)和威廉·D·菲利普斯(William D.Phillips)并列。[4]在一次采访中，朱描述了阿什金最初是如何将光学镊子设想为一种捕获原子的方法的。[5]阿什金能够捕获较大的粒子(直径10到10,000纳米)，但朱负责将这些技术扩展到利用共振激光和磁梯度陷阱捕获中性原子(直径0.1纳米)(参见。磁光陷阱)。

20世纪80年代末，亚瑟·阿什金(Arthur Ashkin)和约瑟夫·M·齐耶季奇(Joseph M.Dziedzic)首次展示了这项技术在生物科学中的应用，他们用这项技术捕获了单个烟草花叶病毒和大肠杆菌。[6]在整个20世纪90年代及之后，卡洛斯·布斯塔曼特、詹姆斯·斯普迪奇和史蒂文·布洛克等研究人员率先使用光学陷阱力光谱来表征分子尺度的生物马达。这些分子马达在生物学中无处不在，负责细胞内的运动和机械动作。光学陷阱使这些生物物理学家能够在单分子水平上观察纳米级马达的力和动力学；自那以后，光学陷阱力谱学使人们更好地理解了这些产生力的分子的随机性质。

光学镊子在生物学的其他领域也被证明是有用的。它们在合成生物学中被用来构建人工细胞的组织状网络[7]，并将合成膜融合在一起[8]以启动生化反应。[7]2003年，光学镊子技术被应用于细胞分选领域；通过在样品区域上创建大的光学强度图案，可以根据细胞的固有光学特性对细胞进行分选。[9][10]光学镊子还被用来探测细胞骨架，测量生物聚合物的粘弹性，[11]并研究细胞的运动性。2011年[12]提出了一种生物分子分析方法，即在靶分子诱导聚集后，对配体包裹的纳米颗粒团进行光学捕获和光学检测[12]，并于2013年进行了实验演示。[13]。

2001年有效演示的卡皮萨-狄拉克效应利用驻波光影响一束粒子束。

研究人员还致力于将光镊子从大型、复杂的仪器转变为更小、更简单的仪器，供那些研究预算较小的人使用。[3][14]。

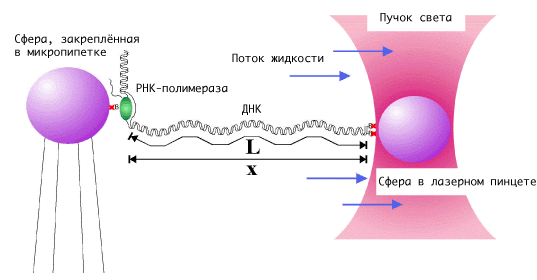
光镊子能够通过高度聚焦的激光束施加极小的力来操纵纳米和微米大小的介电粒子。光束通常通过显微镜物镜聚焦。聚焦光束的最窄处，称为束腰，包含非常强的电场梯度。介质粒子沿梯度被吸引到电场最强的区域，也就是光束的中心。激光还倾向于沿光束传播方向对光束中的粒子施加作用力。这是由于动量守恒：被微小的介电粒子吸收或散射的光子给介电粒子提供动量。这称为散射力，其结果是粒子从梁腰的确切位置向下游稍微偏移，如图所示。

光阱是一种非常灵敏的仪器，能够操纵和探测亚微米介电粒子的亚纳米位移。[15]为此，它们通常用于通过与已连接到单个分子上的珠子相互作用来操纵和研究该分子。DNA和与之相互作用的蛋白质[16]和酶通常都是这样研究的。

对于定量的科学测量，大多数光学陷阱的操作方式是介电粒子很少远离陷阱中心。这样做的原因是，只要位移很小，施加到粒子上的力相对于其从陷阱中心的位移是线性的。这样，一个光阱可以比作一个简单的弹簧，它遵循胡克定律。

对光学捕获行为的正确解释取决于捕获的粒子相对于用于捕获它的光的波长的大小。在颗粒尺寸远大于波长的情况下，简单的射线光学处理就足够了。如果光的波长远远超过粒子的尺寸，粒子可以被视为电场中的电偶极子。对于捕获光束波长数量级内尺寸的介质物体的光学捕获，唯一精确的模型包括使用适当的边界条件处理含时或时间调和的麦克斯韦方程。

在捕获粒子的直径明显大于光波长的情况下，捕获现象可以用射线光学来解释。如图所示，激光器发出的单个光线在进入和离开介质珠子时将被折射。因此，光线将从与其起源方向不同的方向射出。因为光有与之相关的动量，所以方向的改变表明它的动量已经改变。由于牛顿第三定律，粒子上应该有相等和相反的动量变化。

大多数光阱以高斯光束(TEM00模)剖面强度运行。在这种情况下，如果粒子从光束中心移位，如图右侧所示，粒子有一个净力将其返回到陷阱中心，因为强度较高的光束向陷阱中心提供的动量变化比强度较低的光束大，而较弱的光束远离陷阱中心的动量变化较小。净动量变化或作用力使粒子返回陷阱中心。

如果粒子位于光束的中心，则单独的光线通过粒子对称折射，从而不会产生净侧向力。这种情况下的净力是沿着陷阱的轴向的，这抵消了激光的散射力。这种轴向梯度力与散射力的抵消是使珠子稳定地被困在梁腰部下游的原因。

标准镊子的工作原理是沿重力方向传播的俘获激光[17]，而倒装镊子则是逆重力工作的。

在捕获粒子的直径明显小于光波长的情况下，满足瑞利散射条件，可将其视为非均匀电磁场中的点偶极子。施加在电磁场中单个电荷上的力称为洛仑兹力，

F1=Q(E1+dx1dt×B)。{\displaystyle\mathbf{F_{1}}=Q\Left(\mathbf{E_{1}}+{\frac{d\mathbf{x_{1}{dt}}\Times\mathbf{B}\right)。}。

在上面的方程式中，用两项代替电场，一项代表一种电荷，就可以计算出偶极子上的力。偶极子的极化为p=qd，{\displaystyle\mathbf{p}=q\mathbf{d}，其中d{\displaystyle\mathbf{d}}是两个电荷之间的距离。对于一个点偶极子，距离是无穷小的，x 1−x 2。{\displaystyle\mathbf{x}_{1}-\mathbf{x}_{2}。}考虑到两个电荷具有相反的符号，力的形式为。

F=q(E1(x，y，z)−E2(x，y，z)+d(x1−x2)dt×B)=q(E1(x，y，Z)+((x1−x2)⋅∇)E−E1(x，y，z)+d(x1−x2)dt×B。{\displaystyle{\Begin{aligned}\mathbf{F}&；=q\Left(\mathbf{E_{1}}\Left(x，y，z\right)-\mathbf{E_{2}}\Left(x，y，z\right)+{\frac{d(\mathbf{x}_{1}-\mathbf{x}_{2})}{dt}}\次\mathbb。=q\Left(\mathbf{E_{1}}\Left(x，y，z\right)+\Left((\mathbf{x}_{1}-\mathbf{x}_{2})\cot\nabla\right)\mathbf{E}-\mathbf{E_{1}}\Left(x，y，Z\right)+{\frac{d(\mathbf{x}_{1}-\mathbf{x}_{2})}{dt}}\次\mathbf{B}\right)。\end{aligned}。

请注意，E1{\displaystyle\mathbf{E_{1}取消了。乘以电荷q{\displaystyle q}，将位置x{\displaystyle\mathbf{x}}转换为极化p{\displaystyle\mathbf{p}}，

F=(p⋅∇)E+d p dt×B=α[(E⋅∇)E+d E d t×B]，{\DisplayStyle{\Begin{对齐}\mathbf{F}&；=\Left(\mathbf{p}\cdot\nabla\right)\mathbf{E}+{\frac{d\mathbf{p}}{dt}}\次\mathbf{B}\\&；=\alpha\Left[\Left(\mathbf{E}\cdot\nabla\right)\mathbf{E}+{\frac{d\mathbf{E}}{dt。

其中，在第二等式中，假设介电粒子是线性的(即p=αE{\displayStyle\mathbf{p}=\alpha\mathbf{E}})。

在最后一步中，将使用两个等式：(1)矢量分析等式，(2)法拉第归纳定律。

(E⋅∇)E=∇(1 2 E 2)−E×(∇×E){\DisplayStyle\Left(\mathbf{E}\cot\nabla\right)\mathbf{E}=\nabla\Left({\frac{1}{2}}E^{2}\Right)-\mathbf{E}\次\Left(\。Nabla\Times\mathbf{E}\Right)}。

∇×E=−∂B∂t{\DisplayStyle\nabla\Times\mathbf{E}=-{\frac{\Partial\Mathbf{B}}{\Partial t}}。

首先，在上面的力等式的第一项中插入矢量相等。麦克斯韦方程将代替矢量等式中的第二项。然后，可以将包含时间导数的两个项合并为单个项。[18]。

F=α[1 2∇E2−E×(∇×E)+d E dt×B]=α[1 2∇E2−E×(−d B dt)+。DEdt×B]=α[1 2∇E2+ddt(E×B)]。{\displaystyle{\Begin{aligned}\mathbf{F}&；=\alpha\Left[{\frac{1}{2}}\nabla E^{2}-\mathbf{E}\Times\Left(\nabla\Times\mathbf{E}\right)+{\frac{d\mathbf{E}}{dt}}\Times\mathbf{B}\right]\\&；=\alpha\Left[{\frac{1}{2}}\nabla E^{2}-\mathbf{E}\Times\Left(-{\frac{d\mathbf{B}}{dt}}\right)+{\frac{d\mathbf{E}}{dt}}\Times\mathbf{B}\right]\\&；=\alpha\Left[{\frac{1}{2}}\nabla E^{2}+{\frac{d}{dt}}\Left(\mathbf{E}\Times\mathbf{B}\right)\right]。\end{aligned}。

最后一个等式中的第二项是一个量的时间导数，该量通过一个乘法常数与描述单位面积通过曲面的功率的坡印亭矢量相关。由于激光器的功率在远比激光器的光的频率~1014 Hz长得多的频率上采样时是恒定的，这一项的导数平均为零，力可写为[19]。

F=1 2α∇E2=2πn 0 a 3c(m 2−1 m2+2)∇i(R)，{\displaystyle\mathbf{F}={\frac{1}{2}}\alpha\nabla E^{2}={\frac{2\pi n_{0}a^{3}}{c}}\Left({\frac{m^{2}-1}{m^{2}+2}}\right)\nabla I(\mathbf{r})，}。

其中在第二部分中我们已经包括了球形介质粒子的感生偶极矩(以Mks为单位)：α=4πn 0 2ϵ0 a 3(m 2−1)/(m 2+2)E(r，T){\displaystyle\alpha=4\pi n_{0}^{2}\epsilon_{0}a^{3}(m^{2}-1)/(m^{2}+2)\mathbf{E}(\mathbf{r}，t)}，其中a{\displaystyle a}是粒子半径，N0{\displaystyle n_{0}}是粒子的折射率，m=n0/n1{\displaystyle m=n_{0}/n_{1}是粒子与介质的相对折射率，电场大小的平方等于光束强度的平方作为位置的函数。因此，结果表明，当将介质颗粒视为点偶极子时，介质颗粒上的力与沿光束强度方向的梯度成正比。换句话说，这里描述的梯度力倾向于将粒子吸引到强度最高的区域。在现实中，光的散射力与陷阱轴向的梯度力相反，导致平衡位置在强度最大值下游略有偏移。在瑞利近似下，散射力也可以表示为

F scat(R)=k 4α2 6πc n 0 3ϵ0 2 i(R)z^=8πn 0 k 4a 6 3c(m 2−1 m2+2。)2i(R)z^。{\displaystyle\mathbf{F}_{\text{scat}}(\mathbf{r})={\frac{k^{4}\alpha^{2}}{6\pi cn_{0}^{3}\epsilon_{0}^{2}}i(\mathbf{r}){\hat{z}}={\frac{8\pi n_{0}k^{4}a^{6。1}{m^{2}+2}}\right)^{2}i(\mathbf{r}){\hat{z}}。}。

由于散射是各向同性的，所以净动量是向前传递的。在量子水平上，我们将梯度力描述为前向瑞利散射，其中相同的光子同时产生和湮灭，而在散射(辐射)力中，入射光子沿同一方向传播并各向同性地“散射”。由于动量守恒，粒子必须积累光子原始动量，从而在后者中产生向前的力。[20]。

研究高斯光束中原子的相互作用的一个有用的方法是观察原子所经历的强度剖面的谐势近似。在二能级原子的情况下，所经历的势与其交流斯塔克位移有关，

ΔE AC Stark=3πc 2Γμ2ω0 3δi(r，z){\DisplayStyle\mathbf{\DeltaE}_{\Text{AC Stark}}={\frac{3\pi c^{2}\Gamma\u}{2\omega_{0}^{3}\Delta}}\mathbf{i(r，z)}}。

其中Γ{\DisplayStyle\γ}是激发态的自然线宽，μ{\DisplayStyle\µ}是电偶极子耦合，ωo{\DisplayStyle\ω_{o}}是跃迁频率，δ{\DisplayStyle\δ}是激光频率和跃迁频率之间的失谐或差。

高斯光束的强度由波长(λ){\显示样式(\λ)}、最小束腰(Wo){\显示样式(w_{o})}和光束功率(P_O){\显示样式(P_{o})}表征。以下公式定义梁轮廓：

I(r，z)=I0(w0w(Z))2e−2r2w2(Z){\DisplayStyle I(r，Z)=i_{0}\Left({\frac{w_{0}}{w(Z)}}\right)^{2}e^{-{\frac{2r^{2}}{w^{2}(Z)}。

W(Z)=w 0 1+(Z Z R)2{\displaystyle w(Z)=w_{0}{\sqrt{1+\Left({\frac{z}{z_{R}\right)^{2}

P 0=1 2πi 0 w 0 2{\displaystyle P_{0}={\frac{1}{2}}\pi i_{0}w_{0}^{2}}。

为了在光束的径向和轴向上近似该高斯势，当r=0{\DisplayStyle r=0}和z=0{\DisplayStyle z=0}时，强度分布必须分别在z{\DisplayStyle z}和r{\DisplayStyle r}中展开到二阶，并且等于谐势1.2m(ωz 2z2+ωr2r2。){\displaystyle{\frac{1}{2}}m(\omega_{z}^{2}z^{2}+\omega_{r}^{2}r^{2})}。这些展开式是在假定功率固定的情况下进行评估的。

∂2 i∂z 2|r=0=2 P 0λ2π3 w 0 6 z 2=1 2 m DisplayStyle z 2 z 2{\ω{\Partial^{2}i}{\Partial z^{2}{\Biggr|}_{r=0}=。{\frac{2p_{0}\lambda^{2}}{\pi^{3}w_{0}^{6}}z^{2}={\frac{1}{2}}m\omega_{z}^{2}z^{2}}。

∂2 i∂r 2|z=0=4 P 0πw 0 4 r 2=1 2 mωr 2 r 2{\DisplayStyle{\FRAC{\PARTIAL^{2}i}{\PARTIAL R^{2}{\Biggr|}_{z=0}={\FRAC{4p_{0}。}{\pi w_{0}^{4}}r^{2}={\frac{1}{2}}m\omega_{r}^{2}r^{2}}。

这意味着，在求解谐波频率(或考虑原子的光学陷阱时的陷阱频率)时，给出的频率为：

ωr=8 P 0πm w 0 4{\DisplayStyle\omega_{r}={\sqrt{\frac{8p_{0}}{\pi mw_{0}^{4}。

ωz=4 P 0λ2 mπ3 w 0 6{\DisplayStyle\omega_{z}={\sqrt{\frac{4p_{0}\lambda^{2}}{m\pi^{3}w_{0}^{6}。

因此，径向和轴向d的相对陷阱频率

.