遍历经济学:入门
在我之前关于损失厌恶的帖子(这里,这里和这里)中,我预示了一篇文章,即“遍历经济学”可能会揭示我们是否需要损失厌恶来解释人们在不确定情况下的选择。这就是那篇帖子,但我起草的背景材料足够长,足以成为一篇独立的文章。在未来的一篇文章中,我将转向遍历性经济学在损失厌恶中的应用。
下面的大部分摘自Ole Peters和朋友们的演讲和论文,最后是我自己的进化论观点。有关更深层次的潜水,请参阅彼得斯和亚历山大·阿达姆的讲座笔记,或彼得斯最近在“自然物理”中的一篇透视文章。
假设你有100美元,并得到了一场涉及一系列抛硬币的赌博。每翻一次头,你的财富就会增加50%。反面会减少40%。翻100次。
会发生什么事?对于第一次赌博,你有50%的机会获得50美元的收益,也有50%的机会损失40美元。你的预期收益(每个结果按概率加权,0.5*50+0.5*-40)是你财富的5%或5%。未来翻转的绝对赌注大小将取决于过去的翻转,但每翻转一次,你的财富的5%的预期收益是相同的。
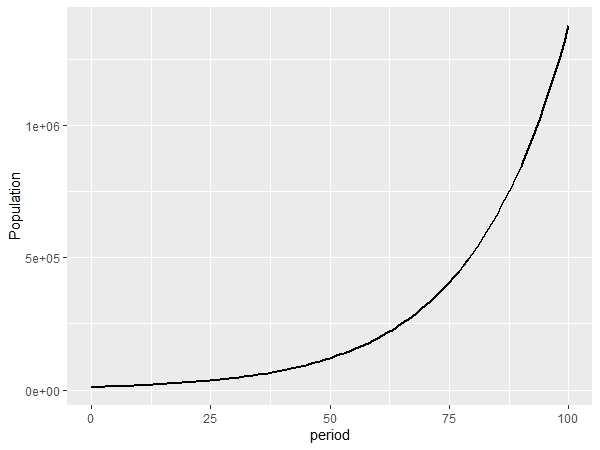
我模拟了10,000个人,每人从100美元开始,每人抛硬币100次。图1中的这条线表示10,000人的平均财富。它看起来很好,尽管有一些波动,但大致按照预期的收益增长,平均财富超过1.6万美元。
拒绝这种赌博的一种解释是避险。厌恶风险的人肯定会认为赌博的预期结果低于相同的金额。
风险厌恶可以通过效用的概念来表示,其中每一级财富都为赌徒提供了主观价值(效用)。如果人们追求效用最大化,而不是赌博的价值最大化,那么人们可能会拒绝下注。
例如,表示风险厌恶个人的一个常见效用函数是取每个财富水平的对数。如果我们将对数效用函数应用到上面的赌博中,赌徒将拒绝掷硬币的提议。[这里的数学计算很简单,赌博的预期效用是0.5*ln(150)+0.5*ln(60)=4.55,这比确定的100美元的效用,ln(100)=4.61要小。]
对于不同的视角,下面是这10,000个人中前20个人的情况。有趣的是,只有两个人的表现好于盈亏平衡(以100美元的黑线表示)。在第100期,最富有的人只有不到1,000美元。
这是怎么回事?第一个图表显示,所有10,000人的平均财富都在增加。当我们观察前20个人时,他们的财富通常会下降。即使是那些赚钱的人赚的钱也比总财富的增长要少。
为了更直观地显示这一点,这里是前20个人的对数比例图,以及全部人口的平均财富。他们的最终财富都低于平均水平。
如果我们检查10000的全部人口,我们会看到一个有趣的模式。平均财富超过16,000美元,但100个周期后的财富中位数为51美分,损失了最初财富的99%以上。54%的人最终拥有的财富不到1.86美元,最终财富低于最初的100美元。然而,171人最终获得了超过1万美元的财富。最富有的人最终拥有1.17亿美元,占总人口财富的70%以上。
对于大多数人来说,这一系列押注是一场灾难。只有在少数人的极好运气和巨额财富的支撑下,它才看起来很好。预期的回报与大多数人的经验不符。
思考正在发生的事情的一种方式是考虑前两个时期可能出现的四种结果。
第一个人有两个头。他们最终拿到了225美元。第二个和第三个人得到正面和反面(顺序不同),最后得到90美元。第四个人最终得到36美元。
这四家公司的平均价格为110.25美元,反映出复合增长率为5%。这是我们积极的一面。但四人中有三人赔钱。随着投机次数的增加,赔钱的比例也会增加,更罕见但更富有的一群人支撑着平均水平。
从很长一段时间来看,一个人往往会得到一半的正面和一半的反面。随着翻转的次数变得无限多,正面和反面的数量“几乎肯定”相等。
这意味着每个人往往会有一半的时间(或初始财富的1.5倍)增加50%,一半的时间(初始财富的60%)减少40%。稍微算算一下,个人财富的时间平均增长是(1.5*0.6)0.5~0.95,或者说每个时期财富大约下降5%。每个人的财富都会以这样的速度缩水。
要获得这方面的直觉,长时间的正面和反面数量相等的运行相当于每两个周期翻转一个正面和一个反面。假设这就是你所做的-翻转头部,然后翻转尾巴。你的财富将在第一轮增加到150美元(100美元*1.5美元),然后在第二轮下降到90美元(150美元*0.6美元)。如果你改变顺序,你会得到同样的结果。实际上,你每两期损失10%(或者说只得到1.5*0.6=0.9)。
时间平均值收敛到集合平均值(我们的人口平均值)的系统称为遍历系统。上面的赌博系统是非遍历的,因为时间平均和整体平均不同。既然我们不能单独体验总体平均水平,我们就不应该被它误导。如果系统是非遍历的,那么像经济学中通常做的那样,关注整体平均可能会产生误导。
当我们看时间平均增长时,我们如何调和这种亏损预期与一些人在100个时期后财富的持续增长?似乎并不是每个人都“几乎肯定”在走向毁灭的道路上。
但他们确实是。如果我们将模拟绘制成1000个周期,而不是100个周期,那么几乎没有赢家。下面是1000个时期人口平均财富的曲线图(前100个是前面显示的),外加一个相同增长的对数曲线图(图4和图5)。
我们可以看到,尽管财富在400年左右达到了一个很大的峰值,但财富最终还是直线下降。1000期间的平均财富为24美元,低于100美元的起始平均值,财富中值为1×10-21(四舍五入到最接近的美分,即为零)。最富有的人拥有24.2万美元,占总财富的98.5%。如果我们再追随这位富人1000代,我预计他们也会被消灭。[我测试了这一点-在2000年期间,最富有的人拥有4×10-7美元。]。尽管期望值为正,但整个人口的财富都被抹去了。
前100个阶段的押注迫使我们在头脑中持有一个违反直觉的想法。当总体人群体验到反映赌注正期望值的结果时,典型的人则不会。总人口财富的增长只是由于少数幸运儿的极端财富。
然而,1000个时期的情况似乎更加令人困惑。押注的正期望值无处可见。怎么会是这样呢?
这个问题的答案在于赌注的分配。在100个周期之后,一个人拥有70%的财富。我们不再像第一轮那样有10,000个同等权重的独立赌注。相反,人们的财富之路在很大程度上取决于这位富人下注的结果。正如我们已经表明的,个人的财富之路几乎肯定会导致5%的复合财富损失。那个人的财富是借来的时间。对于一个人来说,保持财富的唯一方法是押注较小比例的财富,或者通过多次押注来分散财富。
在第一个选项中,凯利标准给出了一个人财富的一部分,他们应该将其作为赌注投入到像这样的正期望值赌注中。凯利标准给出了使财富几何增长率最大化的赌注规模。
B是在下注中收到的净赔率(即在下注的1美元的基础上再获得b美元)。
对于上面的赌注,我们有p=0.5和。正如所提供的那样,我们实际上被要求押注f=0.4,或我们财富的40%,才有机会赢得50%的增长。
然而,如果我们应用上面给出的p和b公式,一个人应该在每一轮下注,或者说10%的财富,以最大化几何增长率。
Kelly准则通过设置下注的大小,有效地最大化了下注的预期对数效用。凯利标准将导致某人想要从任何具有正预期价值的赌注中分得一杯羹。
从长远来看,凯利的赌注“几乎肯定”会带来比任何其他策略都更高的财富。
如果我们模拟上述情景,但每轮只冒财富的10%而不是40%的风险(即正面财富将增长12.5%,反面财富将减少10%),会发生什么?凯利押注的期望值为每轮0.5*0.125+0.5*-0.1=0.0125或1.25%.。下一个数字显示了总体平均值,显示出稳步增长。
如果我们观察这个群体中的个体,我们也可以看到他们的路径更接近于群体平均水平。大多数人的表现仍然低于平均值(系统仍然是非遍历的-时间平均增长率为((1.125*0.9)0.5=1.006或0.6%),并且存在很大的贫富差距,最富有的人在1000期后拥有总财富的36%(100后,他们拥有财富的0.5%)。尽管如此,大多数人还是过得更好,分别有70%和95%的人口在100和1000周期后经历了增长。在1000个时期之后,财富的中位数接近5万美元。
图7:使用Kelly标准的前20个人相对于平均财富的曲线图(对数标尺,1000个周期)。
不幸的是,考虑到我们选择接受还是放弃,涉及我们财富的40%,我们不能使用凯利标准来优化赌注规模,应该拒绝下注。
可用于投资决策的凯利标准的另一个更一般的公式是:
B是您的投资增加的价值(即在您每投资1美元的基础上再获得20亿美元的回报)。
A是如果您输了,您的投资减少的价值(上面的第一个公式假设a=1)。
将此公式应用于本文开头的原始下注,a=0.4,b=0.5,由此f=0.5/0.4-0.5/0.5=0.25或25%。因此,你应该拿出你财富的25%,其中你可能会损失40%或赢得50%。
凯利标准的这一新表述给出了与前者相同的建议,但涉及不同的基线。在第一种情况下,最好的赌注是你财富的10%,这就提供了12.5%的潜在收益。在第二种情况下,你投资25%的财富,可能会获得50%的回报(12.5%的财富)或损失40%的投资(25%的40%,即10%)。尽管建议同样有效,但在一种情况下,你会说f是10%,而在第二种情况下,你会说f是25%。
假设两种类型的代理生活在这个非遍历的世界中,它们的适用性取决于50:50赌注的结果,即50%的收益或40%的损失。一种类型的人总是接受打赌,另一种类型的人总是拒绝打赌。哪一种会成为人口的主宰呢?
对上述例子的直观反应可能是,虽然接受类型的人可能会在短期内获得收益,但从长远来看,他们几乎肯定会把自己赶尽杀绝。有几种情况会出现这种情况。
一种是,特定类型的孩子在随后的投注中都与他们的兄弟姐妹被绑在同一枚硬币上。假设一个人在100个周期后有了100多万个孩子,约占总人口的70%(如果我们借用上面的模拟来描述我们的进化场景,每代人抛一枚硬币,他们就会得到这样的结果)。如果所有人都不得不在第101期及以后押注于完全相同的硬币抛出,那么他们注定要失败。
然而,如果每个孩子都面临自己的掷硬币(比方说,经历特殊的风险),那么崩盘永远不会到来。相反,这些转变的风险是多样化的,人口的增长更接近整体平均水平,即使是在非常长期的情况下也是如此。
下面是模拟100代接受人口的人口图,从10000人开始。对于这个模拟,我假设在每个周期结束时,接受类型的孩子的数量将与他们财富的比例增长相等。例如,如果他们翻头,他们将有1.5个孩子,反之,他们将有0.6个孩子。然后他们就死了。(如果我将孩子的数量设为与这些数字一致的概率,则模拟结果基本相同。)。每个孩子都有自己的翻转动作。
这种进化情景与凯利标准的不同之处在于,接受赌注的类型实际上能够以其包容性适合度的一小部分获得许多独立的赌注份额。
[i]n最大化期望值-赌博期望效用理论所有可能结果的集合平均值-隐含地假设个人可以在平行宇宙(集合中的其他成员)中有效地与自己的副本进行交互。[i]n最大化期望值-赌博期望效用理论的所有可能结果的集合平均值-隐含地假设个人可以与自己的副本有效地交互(集合的其他成员)。非遍历可观测对象的期望值在物理上对应于在许多实体之间汇集和共享。这可能反映了在一个特别设计的大型集体中发生的事情,但它并不反映单个决策者的情况。
对于一个能够在许多后代中分散未来赌注的复制实体来说,他们就能够做到这一点。
有很多皱纹可能会被扔进这个模拟中。一个人要下多少赌注才能重现并有效地多样化他们的未来?赌注越多,糟糕结局的机率就越高。还有一个问题是,孩子们的下注是否真的是独立的(想象一下一个高度相关的部落)。
在我关于这个话题的下一篇帖子中,我问道,鉴于上述情况,我们是否需要风险和损失厌恶来解释我们的选择。
模拟10,000人,他们接受一系列1000个50:50的赌注,以赢得50%的财富或失去40%的财富。
创建一个函数,用于绘制一组时期内人口的平均财富。
创建一个函数,用于绘制群体中的个人在设定时间段内的路径。
使用对数刻度将平均结果和前20个人绘制在同一地块上(图3)。
使用对数图绘制1000个周期的非遍历模拟的平均财富(图5)。