把问题抛诸脑后

Joshua Greene和Andrew Lobb上个月证明了平面上的每条光滑的Jordan曲线和实数上的每条光滑的Jordan曲线，都有四个点形成一个有比率边的矩形。

今天，我们将解释这一结果与奥托·托普利茨著名的“方形钉子猜想”之间的关系，该猜想是在曲线不需要平滑的情况下出现的。

我们在上周四凯文·哈特尼特为广达撰写的一篇文章中注意到了这一点。哈特尼特将这一研究进展描述为大流行的产物，促使他们花时间对根本问题进行更深入的思考。我们想知道在我们自己的领域里，有多少困难的问题在冒泡-这是我们上一篇帖子对(好的)“八卦”感兴趣的原因之一。他还为几何直觉提供了很好的图表。

我们将按照我们最近所说的如何通过寻找和解决简单问题或特殊情况作为垫脚石来解决困难问题的思路来描述这一进展。两年前，迪克写了一篇关于原始Toeplitz问题的帖子，这本书至今仍悬而未决。那篇帖子的重点是乔丹曲线将军可能令人讨厌的地方。这一次需要一个额外的良好条件，但事实证明对所有人来说都是更好的结果。在“良好”方面可以取得多大进展，以“恶劣”来解决问题？这类问题在复杂性理论中经常出现。

约旦曲线是从圆到平面的连续1-1映射的图像。1-1的条件可以防止图像自身相交，因此它是一个单一的闭环。根据乔丹曲线定理，回路总是将平面的其余部分划分为两个连通区域，其中恰好有一个是有界的。令人惊讶的是，一条约旦曲线可以有正的勒贝格测度，但不能充满所有的勒贝格测度。然而，这样的曲线可以接近朱塞佩·皮亚诺定义的那种空间填充曲线，因此任何勒贝格密度都小于威廉·奥斯古德在他1903年的论文中指出的那样。

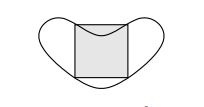
托普利茨猜想，每条乔丹曲线都有四个点组成一个正方形。正如迪克的帖子中指出的那样，正面案例实际上是一个简单的“是”案例。糟糕的情况是曲线无处可微，面积为零。到目前为止，只有在存在限制曲线局部肮脏的一致性条件的情况下，问题才得到肯定的回答。最简单的方法是使曲线平滑，因为它有连续的一阶导数。下面是一条不凸的平滑曲线，因此正方形不需要位于曲线内部：

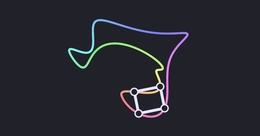
这张图表来自Benjamin Matchske最近对AMS通告中钉住问题的精彩调查。四个月前，我们会说它看起来像是一颗薄薄的心脏或肥大的回旋镖。现在在我们看来它就像一个口罩。

正如调查指出的那样，很容易证明每条约旦曲线都有一些矩形。矩形问题是为了证明每个纵横比的矩形都可以钉在曲线上。正方形和矩形问题变得越来越难有两个主要原因：

尽管任何乔丹曲线都可以写成好的曲线的极限，但是好的曲线中的正方形可以退化到极限中的一个点。

即使对于漂亮的曲线，对于正方形成立的奇偶属性对于矩形也可能失效。