回归和线性组合

最近，我一直在帮助大达纳尔布拉德利和杰克海关组织的线性代数课程，以及几次提出的问题是“为什么程序员应该关心线性组合的概念？”

对于那些不了解的人，给定载体的线性组合是载体的选择，其中一些系数，其将载体以总和重量。

我必须承认，数学书籍做了一个糟糕的绘画概念，因为唯一只需要线性组合只需要证明，而真正的肉是矩阵乘法和交叉产品。但不，线性组合真正躺在许多实际应用的核心。

在某些情况下，算法的整个目标是找到一组矢量的“有用”线性组合。向量是构建块（通常是向量空间或子空间），并且该组线性组合是组合块的法律方式。更简单的块承认更容易和更高效的算法，但它们的线性组合不太表达。因此，权衡。

一个具体的例子是回归。大多数人在线性回归方面的回归。您正在寻找像这样的线性函数近似于一些数据。对于多个变量，您具有例如输入变量的向量，并且作为权重的矢量，并且该功能是。

为了避免偏移（这使得函数仿现而不是纯线性;纯线性函数的公式更容易使用，因为Shift就像一个讨厌的特殊情况，你必须不断考虑），作者通常添加假输入变量这始终固定为1，并重新标记为最终表格。解决的优化问题成为以下内容，您的数据设置为近似的情况。

在这种情况下，正在学习的功能 - 回归的输出 - 不像线性组合。从技术上讲，它是不是以有趣的方式。

当您尝试模拟非线性时，它变得更加明显与线性组合相关。该想法是定义称为基函数的一类功能，并允许您的近似是I.，即B的跨度中的任何功能的任何线性组合。

同样，代替加权输入向量的每个坐标，我们加权每个基本函数的贡献（当给定整个输入向量时）到输出。如果基础函数是输出单个坐标（），则会恢复到线性回归。

然后优化问题是选择权重，以最小化近似的错误。

作为一个例子，让我们说我们希望以二次多项式的基础进行回归。我们的三个输入变量的基础可能看起来像

三个变量中的任何二次多项式都可以作为这些基函数的线性组合写入。另请注意，如果我们将其视为矢量空间的基础，则向量是10个数字的元组 - 多项式中的十个系数。它与载体的条目意味着不同的解释相同。有了这个，我们可以看到我们如何计算Dot产品，预测和其他美好事物，尽管它们可能没有相同的几何敏感性。

这些不是在实践中用于多项式回归的通常基础函数（参见本文末尾的音符），但我们已经在写回归算法中已经造成一些损坏。

虽然有一个封闭的形式解决方案到许多回归问题（包括二次回归问题，但虽然有轻微的扭曲），但梯度下降是一种简单的解决方案来展示如何优化求解器如何找到有用的线性组合。此代码将写入Python 3.9。它在github上。

Linear_combination函数返回一个计算基础函数的加权之和的函数。现在我们可以在数据集中定义错误，以及单点

然后，我们可以定义相对于权重和单个数据点的误差函数的梯度。回想一下，错误函数定义为

由于我们会做随机梯度下降，因此错误公式有点简单。我们计算它不适用于整个数据集，而只有一次只有一个随机点。所以错误是

然后，我们使用链规则计算梯度，使用链规则并注意到为梯度的非零贡献的线性组合的唯一术语是包含的术语。这是使用线性组合的主要好处之一：梯度计算很容易。

线性的另一个优点是该公式对基础函数的含量不可知。只要权重没有出现在基础函数的公式中，这将保持。作为练习：尝试更改实现以在每个数据点周围使用径向基函数。 （在最终看看为什么这在现实生活中会有问题）

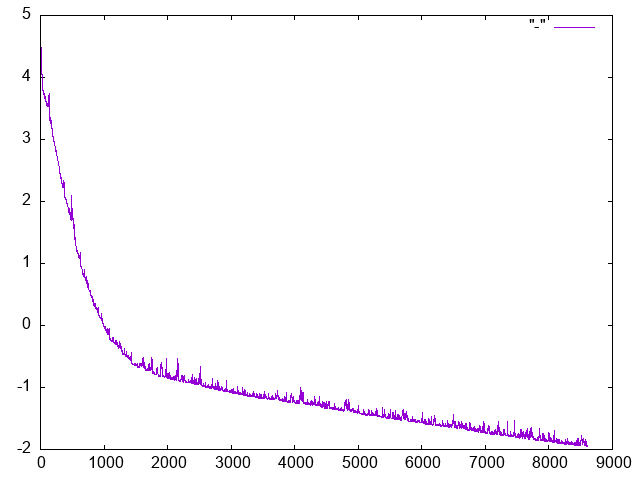
根据随机性，它可能需要几千步，但它通常会收敛到误差的误差; 1.这是对梯度下降步骤的错误的曲线。

真正的多项式内核。我们选择了一套简单的多项式函数。这与“内核”的概念密切相关，但“真实”多项式内核使用略微不同的基函数。它缩放了一些基础函数。这是可以的，因为线性组合可以通过使用适当划分的系数来补偿。但为什么有人想这样做？答案归结为一种称为“核心伎俩”的计算效率技术。简而言之，它允许您在该矢量空间中的两个线性组合之间计算点产品，而无需明确表示空间中的向量开始。如果您的回归算法仅在其代码中使用点产品（根据回归的封闭式解决方案而定），则可以获得非线性特征建模的好处，而无需直接计算功能的成本。这里有很多数学理论（参见再现内核希尔伯特空间），但我现在必须在那里留下它。

径向基函数锻炼有什么问题？ 此练习要求您创建一个基础函数，一个是每个数据点的基本函数。 这里的问题在于，具有如此多的基础函数使线性组合空间太表达。 优化将过度使用数据。 它就像一个查找表：有一个专用于每个数据点的条目。 不在培训中的新数据点很少处理，因为它们不在“查找表”中找到的优化算法。 为了解决这个问题，在实践中，人们将增加一个额外的术语，以对应于权重向量的L1或L2标准的误差。 这允许人们确保重量的总大小很小，并且在L1情况下通常对应于大多数权重为零，并且只有几个权重（最重要的）是非零的。 惩罚线性组合的“幅度”的过程被称为正则化。