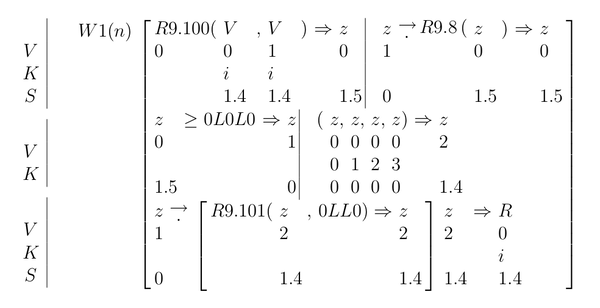禁止提供Konrad Zuse（2014）

康拉德·祖斯（Konrad Zuse）是计算机科学的早期开拓者，尽管他的名字也许不如其他人那么知名。祖斯（Zuse）拥有在40年代制造出第一台可编程计算机Z3以及其他几项计算第一的荣誉。这篇博客文章特别令人感兴趣的是他早期未实现的编程语言Plankalkül 。

像Z3一样，普兰卡库尔（Plankalkül）在许多方面都比它的时代提前。 Zuse的明确目标是能够以较高的级别描述程序，这意味着他包括控制结构和数据类型定义2以及其他在早期计算语言中经常缺少的高级构造。 Zuse在无法使用机器的时候就在Plankalkül上工作，这意味着他的语言工作更具理论性，而不是技术性，因此他允许自己不确定自己如何编程的功能。尽管他的注释已经写在40年代中期，但直到70年代才出版，直到2000年才实施。

当我阅读在打字机3上设置的这种符号的程序时，令我印象深刻的是，某些类型的分组是通过范围的显式指示来处理的：不是像ALGOL风格的语言那样通过匹配的定界符，也不是通过用诸如Python和Haskell之类的语言缩进，但是通过格式化代码，使在代码范围部分的左侧有一条边界：

这是为了捕获以手写或排字法表示的分组方式，并用方括号括起来：

我认为这在概念上很有趣：它就像Python的重要空白，但不是，空白。输入将非常繁琐，但仍与当前的编程符号完全兼容：

春节| @staticmethod | def new_tet（）| | n = randint（0，len（Tet.Tets）-1）| |用于Tet.Tets中的p [n] | | |如果Board.permanent中的p | | | | Game.lose（）| | Game.current = Tet（Tet.Tets [n]，Tet.TetColors [n]）| | def __init __（自身，点，颜色）| | self.points =点| | self.color =颜色

class Tet┃@staticmethod┃def new_tet（）┃n = randint（0，len（Tet.Tets）-1）T在Tet中用于p.Tets [n]┃如果在board.permanent中保留p ┗Game.lose（）┗Game.current = Tet（Tet.Tets [n]，Tet.TetColors [n]）┃def __init __（self，points，color）┃self.points =点┗self。颜色=颜色

然而，看一下这种表示法，我想到了一个有趣的可能性：程序员可以显式地注释有关给定行中涉及的范围类型的信息。在这个类似于Python的示例中，例如，我可以区分使用双行的类作用域，使用粗线的函数作用域和使用细线的控件结构作用域：

类Tet║@staticmethod║def new_tet（）┃n = randint（0，len（Tet.Tets）-1）T在Tet.Tets中用作p [T] [n]┃│如果p在Board.permanent中║ └Game.lose（）┗Game.current = Tet（Tet.Tets [n]，Tet.TetColors [n]）║def __init __（self，points，color）┃self.points =点┗self。颜色=颜色

此方案的一个优点是，孤立地查看了几行，仍然可以清晰地看到周围的内容。例如，我可以单独查看这两行，但仍然可以看出它们在类中声明的函数中使用的控制结构内：

您还可以想象一种假设语言，其中选择范围定界符很重要。在Python中，for和if不会形成新的词汇范围。相反，如果我们可以规定这种符号约定所形成的范围的类型呢？

def okay（）┃如果在函数作用域中声明了True┗n = 5＃n，则返回n＃n从if-scopedef not_okay（）中泄漏出来，如果True┃n = 5＃n在if＆＃中声明了39; s范围┗return n＃错误：此处范围内无n

话虽这么说，但有很多原因使这种表示形式不如现有的表示形式：

它要求程序员逐行注意包围范围的顺序，这通常过于繁琐，对程序员而言并不是特别有用。

选择“哪种范围”的能力绝不能用这种表示法来表达，因为其他语法功能（例如关键字和定界符）可以表达相同的内容。

可以用作作用域标记的线状字符太多，因此该方案不是很可扩展。

它使解析变得复杂（特别是通过引入一类全新的解析错误，其中相邻的行具有不兼容的定界线序列），因此...

复杂的解析错误消息，这是语言UI的重要组成部分，应认真考虑。

因此，就像我之前关于编程语言中的语法案例的文章一样，我敦促读者不要将这种表示法用作编程语言的具体语法。这仅仅是在好奇的符号约定上通过窥镜进行的娱乐性偷看，从未被采用。

就是说：这对于查看代码是一个很好的表示法，程序员不必在代码周围显式绘制ASCII文字。的确，它与Scratch中使用的图形界面相比具有更多的相似之处，Sean McDirmid的“代码排版实验”将这种约定作为一种类似Python的语言在代码上的交互式装饰。

他甚至在斯蒂芬·沃尔夫拉姆（Stephen Wolfram）发表半个世纪之前就撰写了《一种新型科学》。无论如何，从精神上讲，如果把沃尔夫拉姆的自我强化和漂亮的图画都去掉，那本书的其余部分就很像祖斯在1969年出版的著作《 Rehnhender Raum》。

直到50年代后期，才能在其他编程语言中找到数据类型定义。 Zuse对它们的处理非常复杂：Plankalkül对我们现在所说的总和没有任何概念，但是确实有元组形式的乘积。基本类型为S0，它代表一个位，并具有值+和-，因此两位值可能表示为（S0，S0）。包含格式为m×t的数组，表示t的m个重复，而可变长度数组则编码为□×t。包含整数作为原始数，浮点数定义为（3×S0,7×S0,22×S0），代表三个符号位（也可以指示数字是实数还是虚数或零），即七个位指数和22位有效数字。

给出的图像来自Knuth和Pardo的“程序设计语言的早期历史”，它调查了已实现和未实现的早期程序设计语言，并给出了在每个程序语言中都实现的相同基本程序。