类型理论和类型检查器的入门指南

到目前为止，在本系列文章中，我们已经研究了梯度下降的一般原理，以及如何计算前馈神经网络中每一层的反向传播，然后概括了一下CNN中不同类型层的反向传播。

现在，我们将退后一步，从更一般的意义上来看反向传播-通过计算图。通过这一过程，我们将大致了解框架如何计算其

我们将使用LSTM单元作为激励示例-继续对IMDB评论数据集进行情感分析-您可以在随附的Jupyter笔记本中找到代码

让我们回顾一下本系列中使用的原理：

偏导数的直觉：宽松地思考∂y x \ frac {\ partial {y}} {\ partial {x}}∂x y∂量化如果给xxxa一点“轻推”的值，yyy会改变多少。在那时候。

分解计算-我们可以使用链式规则来帮助我们进行计算-而不是一口气尝试计算导数，而是将计算分解为较小的中间步骤。

计算链式规则-当考虑要在链式规则表达式中包含哪些中间值时，请考虑涉及x x x的方程的直接输出-当我们稍微推拉x x x时，其他哪些值会直接受到影响？

一次只包含一个元素-我们不用担心整个矩阵A A A，而是关注元素A i j A_ {ij} A i j。我们将一遍又一遍地引用一个方程式：

C i j = ∑ k A i k B k j C = A。 B C_ {ij} = \ sum_k A_ {ik} B_ {kj} \ iff C = A.B C i j = k A i k B k j C = A。乙

尝试从一个元素到矩阵时，一个有用的技巧是在重复索引（此处为k）上求和-这表明矩阵乘法。

C i j = A i j B i j C = A * B C_ {ij} = A_ {ij} B_ {ij} \ iff C = A * B C i j = A i j B i j⟺C = A * B

完好无损地检查尺寸-检查所有匹配的矩阵的尺寸（派生矩阵应具有与原始矩阵相同的尺寸，并且所有相乘在一起的矩阵应具有对齐的尺寸。

计算图使我们可以清楚地分解计算，并在计算链式规则时查看即时输出。

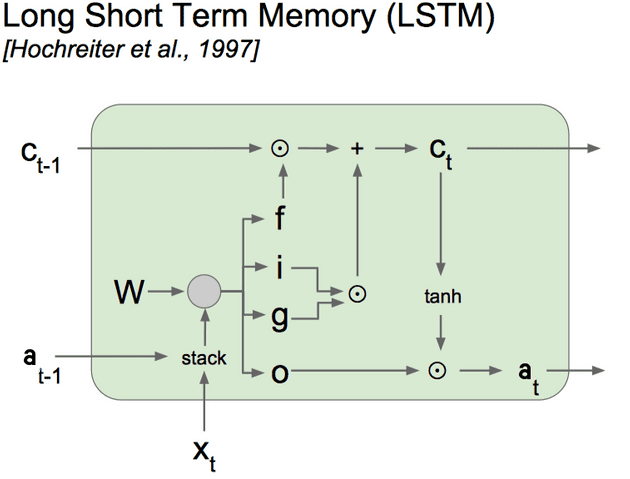
我们将使用LSTM的计算图表示形式（如上所示），通过时间的反向传播来计算梯度。

从上一篇文章开始，LSTM中一个时间步的正向传播方程为：

Γi =σ（W i。[a＆lt; t − 1＆gt;，x＆lt; t＆gt;] + bi）\ Gamma_i = \ sigma（W_i。[a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] + b_i）Γi =σ（W i。[a＆lt; t − 1＆gt;，x＆lt; t＆gt;] + bi）

Γf =σ（W f。[a＆lt; t-1＆gt;，x＆lt; t＆gt;] + bf）\ Gamma_f = \ sigma（W_f。[a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] + b_f）Γf =σ（W f。[a＆lt; t − 1＆gt;，x＆lt; t＆gt;] + bf）

Γo =σ（W o。[a＆lt; t − 1＆gt;，x＆lt; t＆gt;] + bo）\ Gamma_o​​ = \ sigma（W_o。[a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] + b_o）Γo =σ（W o。[a＆lt; t − 1＆gt;，x＆lt; t＆gt;] + bo）

c〜＆lt;吨= tanh⁡（W c。[a＆lt; t − 1＆gt;，x＆lt; t＆gt;] + b c）\ tilde {c} ^ {＆lt; t＆gt;} = \ tanh（W_c。[a ^ {＆lt; t-1>}，x ^ {＆lt; t＆gt;}] + b_c）c〜＆lt;吨= tanh（W c。[a＆lt; t − 1＆gt;，x＆lt; t＆gt;] + b c）

c ＜吨=Γi ∗ c〜＆lt;吨+Γf ∗ c＆lt; t − 1＆gt; {c} ^ {＆lt; t＆gt;} = \ Gamma_i * \ tilde {c} ^ {＆lt; t＆gt;} + \ Gamma_f * {c} ^ {＆lt; t-1＆gt;} c＆lt;吨=Γi ∗ c〜＆lt;吨+Γf ∗ c＆lt; t − 1＆gt;

＆lt;吨=Γo tanh⁡c＆lt;吨a ^ {＆lt; t＆gt;} = \ Gamma_o​​ * \ tanh {c} ^ {＆lt; t＆gt;} a＆lt;吨=Γo ∗ tanh c＆lt;吨

[a＆lt; t − 1＆gt; ，x ＜吨] [a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] [a＆lt; t − 1＆gt; ，x ＜吨]表示两个矩阵的级联以形成（n a + n x）（n_a + n_x）（n a + n x）x m m m矩阵。一种 。 B A.B A。 B表示A A A和B B B的矩阵乘法，而A * B A * B A * B表示元素乘法。 Γ\ GammaΓ是指门-有关所使用符号的完整分类，请参见上一篇文章定义LSTM。

给定相对于＆lt; 2的梯度，以反向传播通过该单元。吨a ^ {＆lt; t＆gt;} a＆lt;吨和c＆lt;吨c ^ {＆lt; t＆gt;} c＆lt;吨从下一步的反向传播中，我们需要计算每个权重W i，W f，W o，W c W_i，W_f，W_o，W_c W i，W f，W o，W的梯度c并对bi，bf，bo，bc b_i，b_f，b_o，b_c bi，bf，bo，bc进行偏置，最后我们需要向后传播到上一个时间步长并计算关于a＆lt; ; t − 1＆gt; a ^ {＆lt; t-1＆gt;} a＆lt; t − 1＆gt;和c＆lt; t − 1＆gt; c ^ {＆lt; t-1＆gt;} c＆lt; t-1＞。

这些是很多要计算的偏导数-实际上，随着我们的神经网络变得越来越复杂，将会有更多的偏导数要计算。

首先，由于门方程是相同的，我们可以将它们组合起来，所以我们有一个3 na 3n_a 3 na xmmm矩阵Γ\ GammaΓ包含三个门的输出，我们可以引用矩阵Γi的前三分之一\ Gamma_iΓi和另外三分之二Γf \ Gamma_fΓf和Γo \ Gamma_o​​Γo。那么我们有一个3 na 3n_a 3 na x（na + nx）（n_a + n_x）（na + nx）权重矩阵W g W_g W g和一个3 na 3n_a 3 na x 1 1 1偏置向量bg b_g bg。

接下来，我们要记录计算中的所有中间阶段（图中的每个节点）。

我们将＆lt; t − 1＆gt; a ^ {＆lt; t-1＆gt;} a＆lt; t − 1＆gt;并且x ＜吨x ^ {＆lt; t＆gt;} x＆lt;吨形成（n a + n x）（n_a + n_x）（n a + n x）x m m m级联的输入矩阵[a＆lt; t − 1＆gt; ，x ＜吨] [a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] [a＆lt; t − 1＆gt; ，x ＜吨]。

我们使用权重W g W_g W g和偏差b g b_g b g来计算门Z g Z_g Z g的加权输入矩阵。

同样，我们计算候选存储器c〜＆lt;的加权输入Z c Z_c Z c。吨\ tilde {c} ^ {＆lt; t＆gt;} c〜＆lt;吨使用权重矩阵W c W_c W c和偏差b c b_c b c。

（注意：该图使用一个权重矩阵W，但由于使用的激活函数不同，因此有助于分别考虑这些权重）

我们将S型激活函数应用于Z g Z_g Z g以获得门矩阵Γ\ GammaΓ（在图中用f，i，o表示），tanh激活函数应用于Z c Z_c Z c以获得c〜 ＆lt;吨\ tilde {c} ^ {＆lt; t＆gt;} c〜＆lt;吨（在图中用g表示）。

由于逐元素的乘法和加法是简单的运算，为简便起见，我们将不给出中间输出Γi * c〜＆lt;吨\ Gamma_i * \ tilde {c} ^ {＆lt; t＆gt;}Γi ∗ c〜＆lt;吨并且Γf ∗ c＆lt; t − 1＆gt; \ Gamma_f * {c} ^ {＆lt; t-1＆gt;}Γf ∗ c＆lt; t − 1＆gt;自己的符号。

现在，我们将计算图分解为步骤，并添加了中间变量，我们得到了以下等式：

Z g ＝ W g。 [a＆lt; t − 1＆gt; ，x ＜吨] + b g Z_g = W_g。[a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] + b_g Z g = W g。 [a＆lt; t − 1＆gt; ，x ＜吨] + b g

Z c = W c。 [a＆lt; t − 1＆gt; ，x ＜吨] + b c Z_c = W_c。[a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] + b_c Z c = W c。 [a＆lt; t − 1＆gt; ，x ＜吨] + b c

c ＜吨=Γi ∗ c〜＆lt;吨+Γf ∗ c＆lt; t − 1＆gt; {c} ^ {＆lt; t＆gt;} = \ Gamma_i * \ tilde {c} ^ {＆lt; t＆gt;} + \ Gamma_f * {c} ^ {＆lt; t-1＆gt;} c＆lt;吨=Γi ∗ c〜＆lt;吨+Γf ∗ c＆lt; t − 1＆gt;

这些方程式对应于图中的节点-左侧变量是节点的输出边，右侧变量是节点的输入边。

这些方程使我们在计算链式规则时可以清楚地看到变量的即时输出-例如对于[＆lt; t − 1＆gt; ，x ＜吨] [a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] [a＆lt; t − 1＆gt; ，x ＜吨]立即输出是Z g Z_g Z g和Z c Z_c Z c。

如果我们看方程式/计算图，我们通常可以看一下运算的类型，然后使用相同的标识：

加法：如果C = A + BC = A + BC = A + B，则∂C∂A = 1 \ frac {\ partial {C}} {\ partial {A}} = 1∂A∂C = 1和∂ C∂B = 1 \ frac {\ partial {C}} {\ partial {B}} = 1∂B∂C = 1

元素乘法：如果C = A * BC = A * BC = A ∗ B，则∂C∂A = B \ frac {\ partial {C}} {\ partial {A}} = B∂A∂C = = B ∂C∂B = A \ frac {\ partial {C}} {\ partial {B}} = A∂B∂C = A

tanh：如果C = tanh⁡AC = \ tanh AC = tanh A，则∂C∂A = 1-tanh⁡2 A = 1-C 2 \ frac {\ partial {C}} {\ partial {A}} = 1 -\ tanh ^ 2 A = 1-C ^ 2∂A∂C = 1 = tanh 2 A = 1 − C 2

乙状结肠：如果C =σ（A）C = \ sigma（A）C =σ（A），则∂C∂A =σ（A）−σ2（A）= C ∗（1 − C）\ frac {\部分{C}} {\部分{A}} = \ sigma（A）-\ sigma ^ 2（A）= C *（1-C）∂A∂C = =σ（A）−σ2（A） = C ∗（1 − C）

加权输入：这与前馈神经网络相同。如果Z = W。 X + b Z = W.X + b Z = W。 X + b然后：

∂J∂W = 1 m∂J∂Z。 XT \ frac {\ partial {J}} {\ partial {W}} = \ frac {1} {m} \ frac {\ partial {J}} {\ partial {Z}}。X ^ {T}∂W ∂J = m 1∂Z∂J。 T

∂J∂b = 1 m ∑ i = 1 m∂J f Z \ frac {\ partial {J}} {\ partial {b}} = \ frac {1} {m} \ sum_ {i = 1} ^ { m} \ frac {\ partial {J}} {\ partial {Z}}∂b∂J = m 1 i = 1 m∂Z∂J

∂X = W T。 ∂J∂Z \ frac {\ partial {J}} {\ partial {X}} = W ^ {T}。\ frac {\ partial {J}} {\ partial {Z}}∂X∂J = WT 。 ∂Z∂J

有了这些通用的计算图原理，我们就可以应用链式规则。我们对偏导数进行元素乘（∗ * ∗），即

∂J∂A =∂J∂B ∗∂B∂A \ frac {\ partial {J}} {\ partial {A}} = \ frac {\ partial {J}} {\ partial {B}} * \ frac {\ partial {B}} {\ partial {A}}∂A∂J = =∂B∂J ∗∂A∂B

因此，如果B = f（A）B = f（A）B = f（A）且C = g（A）C = g（A）C = g（A），即BBB和CCC是AAA中的立即输出计算图，然后将偏导数求和：

∂J∂A =∂J∂B ∗ B∂A +∂J∂C ∗∂C∂A \ frac {\ partial {J}} {\ partial {A}} = \ frac {\ partial {J}} {\ partial {B}} * \ frac {\ partial {B}} {\ partial {A}} + \ frac {\ partial {J}} {\ partial {C}} * \ frac {\ partial {C} } {\ partial {A}}∂A∂J = = B B∂J ∗∂A∂B +∂C∂J ∗∂A∂C

在TensorFlow或Keras之类的深度学习框架中，每个可区分的操作都将具有这样的身份。

尝试计算∂J∂A \ frac {\ partial {J}} {\ partial {A}}∂A∂J时，我们将使用以下一般公式：

∂J∂A =∂J∂B ∗∂B∂A \ frac {\ partial {J}} {\ partial {A}} = \ frac {\ partial {J}} {\ partial {B}} * \ frac {\ partial {B}} {\ partial {A}}∂A∂J = =∂B∂J ∗∂A∂B

为简便起见，我们将使用上述操作的标识替换∂B∂A \ frac {\ partial {B}} {\ partial {A}}∂A∂B的值。

∂J〜a〜＆lt;吨=∂J＆lt;吨∗Γo \ frac {\ partial {J}} {\ partial {\ tilde {a} ^ {＆lt; t＆gt;}}} = \ frac {\ partial {J}} {\ partial {a ^ {＆lt; t＆gt;}}} * \ Gamma_o​​∂a〜＆lt;吨∂J = a＆lt;吨∂J ∗Γo

∂JΓo =∂J∂a＆lt;吨* a〜＆lt;吨\ frac {\ partial {J}} {\ partial {\ Gamma_o​​}} = \ frac {\ partial {J}} {\ partial {a ^ {＆lt; t＆gt;}}} * \波浪号{a} ^ {＆lt; t＆gt;}∂Γo∂J = = a a＆lt;吨∂J ∗ a〜＆lt;吨

使用方程式6，并将方程式5写为c ＜c的方程式。 t + 1＆gt; c ^ {＆lt; t + 1＆gt;} c＆lt; t + 1＆gt;而不是c＆lt;吨c ^ {＆lt; t＆gt;} c＆lt;吨（即在时间步长上加1）：

∂c＜吨=∂c＆lt; t + 1＆gt; *Γf +∂J∂a〜＆lt;吨∗（1 − a〜＆lt; t＆gt; 2）\ frac {\ partial {J}} {\ partial {c ^ {＆lt; t＆gt;}}} = \ frac {\ partial {J}} {\ partial {c ^ {＆lt; t + 1＆gt;}}} * \ Gamma_f + \ frac {\ partial {J}} {\ partial {\ tilde {a} ^ {＆lt; t（＆gt;}}} *（1- \ tilde {a} ^ {＆lt; t＆gt; 2}）∂c＆lt;吨∂J = c＆lt; t + 1＆gt; ∂J ∗Γf + + a a＆lt;吨∂J ∗（1 − a〜＆lt; t＆gt; 2）

∂J c〜＆lt;吨=∂c＆lt;吨∗ i i \ frac {\ partial {J}} {\ partial {\ tilde {c} ^ {＆lt; t＆gt;}}} = \ frac {\ partial {J}} {\ partial {c ^ {＆lt; t＆gt;}}} * \ Gamma_i∂c〜＆lt;吨∂J = c＆lt;吨∂J ∗Γi

∂J∂i =∂C∂＆lt;吨* c〜＆lt;吨\ frac {\ partial {J}} {\ partial {\ Gamma_i}} = \ frac {\ partial {J}} {\ partial {c ^ {＆lt; t＆gt;}}} * \ tilde {c} ^ {＆lt; t＆gt;}∂i =∂c＆lt;吨∂J ∗ c〜＆lt;吨

∂JΓf =∂J∂c＆lt;吨* c＆lt; t − 1＆gt; \ frac {\ partial {J}} {\ partial {\ Gamma_f}} = \ frac {\ partial {J}} {\ partial {c ^ {＆lt; t＆gt;}}} * c ^ {＆lt; t-1＆gt;}∂Γf J = c＆lt;吨∂J ∗ c＆lt; t − 1＆gt;

∂J∂Z g =∂J∂ΓΓ∗（1 −Γ）\ frac {\ partial {J}} {\ partial {Z_g}} = \ frac {\ partial {J}} {\ partial {\ Gamma }} * \ Gamma *（1- \ Gamma）∂Z g∂J = =ΓΓJ ∗Γ∗（1 −Γ）

∂Z c = c c〜＆lt;吨∗（1 − c〜＆lt; t＆gt; 2）\ frac {\ partial {J}} {\ partial {Z_c}} = \ frac {\ partial {J}} {\ partial {\ tilde {c} ^^ { ＆lt; t＆gt;}}} *（1- \ tilde {c} ^ {＆lt; t＆gt; ^ 2}）∂Z c∂J =∂c〜＆lt;吨∂J ∗（1 − c〜＆lt; t＆gt; 2）

公式1和2相同，偏导数也相同，只是下标不同。

∂J∂W g = 1 m∂J∂Z g。 [a＆lt; t − 1＆gt; ，x ＜吨] T \ frac {\ partial {J}} {\ partial {W_g}} = \ frac {1} {m} \ frac {\ partial {J}} {\ partial {Z_g}}。[a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] ^ T∂W g∂J = m 1∂Z g∂J。 [a＆lt; t − 1＆gt; ，x ＜吨] T

∂J bg = 1 m ∑ i = 1 m∂Z g（i）\ frac {\ partial {J}} {\ partial {b_g}} = \ frac {1} {m} \ sum_ {i = 1} ^ {m} \ frac {\ partial {J}} {\ partial {Z_g ^ {{i}}}}}∂bg∂J = m 1 i = 1 m∂Z g（i） ∂J

∂J∂Wc ＝1m∂J∂Zc。 [a＆lt; t − 1＆gt; ，x ＜吨] T \ frac {\ partial {J}} {\ partial {W_c}} = \ frac {1} {m} \ frac {\ partial {J}} {\ partial {Z_c}}。[a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}] ^ T∂W c∂J = m 1∂Z c∂J。 [a＆lt; t − 1＆gt; ，x ＜吨] T

∂J bc = 1 m ∑ i = 1 m∂Z c（i）\ frac {\ partial {J}} {\ partial {b_c}} = \ frac {1} {m} \ sum_ {i = 1} ^ {m} \ frac {\ partial {J}} {\ partial {Z_c ^ {（i）}}}}∂bc∂J = m 1 i = 1 m∂Z c（i） ∂J

∂J∂[a＆lt; t − 1＆gt; ，x ＜吨] ＝ W g T。 ∂J∂Z g + W c T。 ∂J∂Z c \ frac {\ partial {J}} {\ partial {[a ^ {＆lt; t-1＆gt;}，x ^ {＆lt; t＆gt;}]}} = W_g ^ T。\ frac {\ partial {J}} {\ partial {Z_g}} + W_c ^ T。\ frac {\ partial {J}} {\ partial {Z_c}}∂[ ＆lt; t − 1＆gt; ，x ＜吨]∂J = W g T。 ∂Z g∂J + W c T。 ∂Z c∂J

因此，通过将计算图分解为多个步骤，我们可以将计算分解为更小的更简单的步骤，而仅使用上述操作的派生身份。 我们看到的激励性示例使用LSTM网络对IMDB评论数据集进行情感分析 ＃我们计算dC＆lt; t＆gt; 因为我们都需要dC＆lt; t + 1＆gt; 和dA ＜ t＆gt; ＃关于IFO门的输出的导数-滥用表示法称为dIFO ＃关于门的未激活输出的导数（在应用S型信号之前） 今年夏天，我正在用自己的博客讲授我今年学到的主题。 这是双赢的局面-您可以获得计算机科学教程，并且可以与您分享！ 在检查反向支撑方程式时，有一个数字检查器会很有帮助-我在随附的Jupyter笔记本中写了一个数字检查器。

我们开始研究该系列中最常用的术语，然后研究林中的简单机器学习算法。 ......