兰姆达微积分的乐趣

1935年，一位名叫阿隆佐·丘奇的绅士想出了一个可以计算…的简单方案。几乎什么都行。他的方案被称为兰姆达微积分(Lambda Calculus)。这是一项非凡的创新，因为他甚至没有电脑来测试他的想法。更酷的是，这些想法在今天影响着我们：任何时候你使用一个函数，你都应该向丘奇先生致敬。

Lambda演算是如此酷，以至于许多黑客将其用作秘密握手--如果你愿意的话，这是一个“谨慎的信号”。当然，最著名的是PG的Y组合器。在这篇文章中，我们将找出它的全部内容，并用我们从未想象过的功能来做一些事情。最后，您将构建几乎所有的编程概念：数字、布尔值，您可以将其命名为…。只需使用函数即可。

开SUV的城市居民很少认为他们的汽车是穿越多岩石的沙漠和洪水泛滥的河流的凶猛机器。程序员和函数也是如此。下面是我们认为函数的作用：

安全、干净、有用。我们已经习以为常了，如果我们发现我们可以用无数种方法来弯曲函数来做任何事情，那会让我们大吃一惊。

让我们到荒野里走一走吧。假设您想为Pair创建一个数据结构：

你会怎么做呢？使用地图、类或记录来表示一对是明智的。但是…。您也可以使用函数。

现在我们的前搭档接受一个选择器参数。如果我们用这个选择器运行前任配对会怎么样：

这正好给我们带来了我们这双鞋的第一个价值！我们可以用它来编写教堂优先函数：

我们只是用函数来表示对。现在，由于Lisp的语法只是一堆组合在一起的对，这也意味着我们可以表示Lisp…的语法。功能齐全！

我们刚才所做的类似于一个城市居民驾驶他们的越野车…。在一个下雪的日子里。它变得更疯狂了。

这就是我们能做的。让我们取一个我们熟悉和喜爱的函数，并在Lambda演算中自上而下地实现它。

在本文结束时，我们将只使用函数构建阶乘。

为了做到这一点，我想走到前面说我有一点作弊。在丘奇的Lambda演算中，没有定义，所有函数都有一个参数。以下是他所说的：

在他的规则中，您通过在前面弹出一个小λ来定义匿名函数。下面是参数，后面跟着一个。.在..之后。是应用程序。

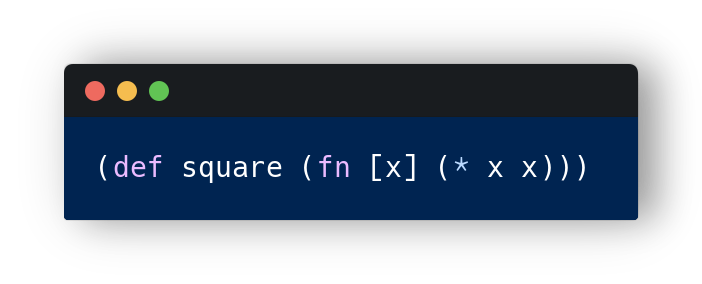
这非常类似于clojure中的单参数匿名函数：λx.x=>；(fn[x]x)。

我们可以遵循这些规则，但是像那样编写阶乘将很难很快得到推理。让我们稍微调整一下规则。这些更改不会影响Lambda演算的本质，但会使我们更容易考虑代码。它是这样的：

1)对于单参数函数，(fn[x]x)很好地映射到Church的编码。我们可以继续按原样使用它。

2)由于Church的lambdas只接受一个参数，要用两个参数表示一个函数，他必须编写两个匿名函数：

但是，在Clojure 1中，像这样嵌套我们的函数可能会很烦人。为了让我们的工作更轻松，我们将允许使用多参数函数：

3)最后，除了函数定义提供的变量之外，Church没有变量的概念。

为了使我们的代码保持正常，我们将允许def，但有一条规则：

您可以使用def，只要您可以用匿名函数“替换”它并且没有中断。

这将中断，因为如果我们替换(定义Make-Pair…)。使用匿名函数，将不再有名为Make-Pair的变量！

就是这样，这是我们的规矩。有了这些，我们就可以做阶乘了！

我们首先需要的是数字的概念。我们怎么能做到这一点呢？

丘奇想到了一个很酷的主意。如果是“Numbers”，其中高阶函数有两个参数：函数f和值v，情况会怎样呢？

(def零(fn[f v]v))(def one(fn[f v](f(零f v)(def Two(fn[f v](f(One F V)。

我们可以通过“计数”f被合成的次数来计算出每个函数代表的数字。

例如，0将合成f的次数为零：它只返回v。1，将合成f一次：(Fv)。2将组成两次：(F(f，v))，依此类推。

为了帮助我们在REPL中查看这些数字，让我们创建一个快速转换器函数：

因为教堂数字由它被调用的次数组成，其中v是第一个参数，所以我们需要知道它在Clojure中是什么数字，只需提供Inc作为f，提供0作为v！例如，现在2将做(Inc(Inc0))，并为我们获得相应的Clojure编号。

我们在这里做的是委托f组成前面的数字(在本例中是1)，然后再调用f一次。

瞧啊。给这个函数一个数字，它将返回一个新的数字，并再次调用f。我们刚刚发现了Inc.！

现在我们有了这个函数，我们还可以编写一个快速帮助器将Clojure数字转换为这些数字：

接下来，我们需要一种方法来“递减”一个数字。嗯，使用Inc，我们再一次创建一个组成f的数字。如果我们能少做一次组成f的函数，那么我们就有了dec！

还记得我们的配对数据结构吗？让我们为它创建一个函数(我们稍后会用到这个函数)：Shift-and-Inc。它所要做的就是取一对数字，并将这对数字“前移”一位：

例如，对(0 1)应用Shift-and-Inc将生成(1 2)。再一次，它将产生(2 3)，依此类推。

班姆，我们拿一双。第二件物品被移到第一个位置，并被它的刻痕朋友取代。让我们试试看：

(设[p(Shift-and-Inc(教堂对一二))](映射教堂数字->；int[(教堂第一个p)(教堂第二个p)]))；=>；(23)。

请记住，我们的教堂数字将调用Shift-and-Inc N次，表示其数值。如果我们从一个对(0，0)开始，那么如果我们将Shift-and-Inc.组合N次，那么结果b会是什么呢？

我们的结果将是对(N-1，N)。这意味着如果我们把我们对的第一部分取走，我们就有了12月！

接下来是乘法。假设我们用a乘以b，我们需要产生一个教会数字，组成f，a*b次。要做到这一点，我们可以利用以下想法：

假设我们做了一个函数g，它组成了f，b次。如果我们把这个函数提供给a，它会调用g，a次。

如果a是“2”，“b”是3，f会合成几次？嗯，g会组成两次。每次合成g，就合成f 3次。一共出了6次！

我们有数字，我们有*，我们有12月。Next Up…。布尔人！

他们接受一个“真”案和一个“假”案。我们的chorge-true函数将返回true case，而chocket-false函数将返回false case。

就这样。令人惊讶的是，这足以处理布尔值。下面是我们如何将它们转换为Clojure bools。

我们的教堂-true将返回第一个参数(True)，而我们的教堂-false将返回第二个参数！

他们看起来眼熟吗？这就是我们教会第一和教会第二的选择器功能！如果我们愿意，我们可以互换它们，😮。

如果你和我一样，你对那些布尔人有点怀疑。让我们好好利用它们，平息我们的恐惧吧。下面是如何创建If结构的方法：

我们要做的所有事情就是简单地将事物打乱，并向我们的布尔值提供When-True和When-False的情况！Church-true将返回When-True大小写，而Church-False将返回When-False大小写。

我们几乎拥有实现阶乘所需的所有构造。少了一块：零块？我们需要一种方法来判断数字何时为零。

如果一个数字大于零，则会调用f，这会将v替换为chocket-false。否则，我们将返回v的初始值，教堂为真。

嗯，我们有数字，我们有如果，我们有零？我们有*，我们有12月。我们可以这样翻译：

(def阶乘-V0(Fn[教会数字-n](教会-IF(教会-零？教堂数字-n)(fn[]one)(fn[](教堂-*教堂数字-n(阶乘-v0(教堂-十二月教堂-数字-n)。

唯一奇怪的是，我们将WHEN-TRUE和WHEN-FALSE案例包装在一个匿名函数中。这是因为我们的教会IF与Clojure的IF略有不同。Clojure的IF只评估WHEN-TRUE和WHEN-FALSE案例中的一个。我们的方法对这两种情况都求值，这会触发无限递归。我们通过将两种情况都包装在一个lambda中来避免这一点，这会“延迟”我们的评估。2个

好的，差不多了。我们作弊了。记住我们的规则3：如果我们用匿名函数替换变量，一切都应该正常工作。如果我们将阶乘-V0编写为匿名函数，会发生什么情况？

(fn[教堂-数字-n]((教堂-IF(教堂-零？教堂数字-n)(fn[]one)(fn[](教堂-*教堂数字-n；：<；：<；呃oh(factorial-v0(教堂-12月教堂-数字-n)。

这里有一种我们可以解决的方法。我们可以更新这一点，这样阶乘就可以作为参数提供给它自己。

(Fn[阶乘-Cb](Fn[教会数字-n])((教会-IF(教会-零？教堂数字-n)(fn[]one)(fn[](教堂-*教堂数字-n(factorial-cb(教堂-12月教堂-数字-n)？)。

那是可行的，但我们只是把问题轻描淡写。他妈的会怎么做？是吗？我们需要某种方式将阶乘的引用传递给它本身！

让我们看看我们能不能把这件事办好。首先，让我们编写阶乘，它接受自身的某种“可注入”版本：

(def可注射-阶乘(Fn[阶乘-Cb](Fn[教会数字-n])((教会-IF(教会-零？教堂数字-n)(fn[]one)(fn[](教堂-*教堂数字-n(阶乘-cb(教堂-十二月教堂-数字-n)。

好的，我们现在所做的就是将问题转移到这个Make-Recursable函数😅中。请耐心听我说。

让我们想象一下解决方案需要看起来是什么样子。我们希望使用某个阶乘cb函数调用injectable-f来处理“下一次调用”。

这似乎是对的。请注意注释递归处理程序。这是针对此表单的：

如果我们以某种方式访问此表单，我们可以在？！中使用它。好吧，让我们把这个问题再说一遍：

在这里，我们将递归处理程序包装到一个函数中。如果它能自己复制一份，我们就大功告成了。但这意味着我们又回到了同样的问题上：我们如何才能给递归处理程序一个自身的副本呢？这里有一个想法：

(def make-recursable(fn[Injectable-f]((fn[递归处理程序](递归处理程序递归处理程序)(fn[递归处理程序](Injectable-f(Fn[Next-Arg]((递归处理程序递归处理程序)Next-Arg)。

这将最终产生一个具有阶乘CB的新阶乘函数。然后我们就用Next-Arg来称呼它，让派对继续进行下去！

这个Make-Recursable函数也称为Y组合器。你可能听说过很多关于它的事情，这个例子可能很难效仿。如果你想了解更多，我推荐吉姆的主题演讲。

哇，我们做到了。我们刚刚编写了阶乘，所有我们使用的都是匿名函数。为了证明这一点，让我们删除一些规则。下面是我们的代码在没有任何变量定义的情况下将如何结束：

(教堂-数字->；Int(Fn[Injectable-f]((Fn[递归处理程序](递归处理程序递归处理程序)(Fn[递归处理程序](Injectable-f(Injectable-f(Fn[Next-Arg]((递归处理程序递归处理程序)Next-Arg)(Fn[阶乘-Cb](Fn[教堂数字-n](Fn[教堂布尔When-true When-False](教堂布尔When-True-False)。TRUE WHEN-FALSE))((FN[教堂编号](教堂编号(FN[v](Fn[WHEN-TRUE WHEN-FALSE]WHEN-FALSE]WHEN-FALSE))(FN[WHEN-TRUE WHEN-FALSE]WHEN-TRUE)教堂编号-n)(FN[](Fn[](Fn[f v](f((Fn[f v]v)f v)(Fn[]((Fn。[num-a num-b](fn[fv](num-a(部分num-bf)v))教堂数字-n(阶乘-cb((fn[教堂数字]((fn[a b]a)(教堂数字(fn[对](fn[b]a))((fn[b]((fn[a b](fn[选择器](选择器a b)(fn[对。](Pair(Fn[a b]b))Pair)((Fn[教堂数字](Fn[f v](f(教堂数字f v)((Fn[Pair](Pair(Fn[a b]b)((Fn[a b](Fn[选择器](选择器a b)(Fn[f]v)(fn[f]v)(fn[f]。V)教堂编号-n)((fn[教堂编号](fn[f v](f(教堂编号f v)((fn[教堂编号](fn[f v](f(教堂编号f v)((fn[教堂编号](fn[f v](f(教堂编号f v)(fn。[fv](f((fn[fv](f((fn[fv]v)fv)。

我们刚刚把我们的任务带过了莫哈韦沙漠！我们制作了数字、布尔值、算术和递归…。全部来自匿名函数。希望你玩得开心！如果您想查看完整的代码，请查看GH回购。

我将带着一些Clojure宏观乐趣离开。当用匿名函数“替换”所有Deff的时候，我们是如何做到的呢？

在较弱的语言中，我们可能需要手动复制粘贴3。在LISP中，我们可以使用宏。

首先，让我们重写def。此版本将每个def的源代码“存储”为元数据：

(def宏def#"；`def`周围的轻型包装，用于跟踪此let的每个定义的_source code_后面的us_unwork_all定义：>；"；[name v]`(do(def~name~v)(alt-meta！(var~name)assoc：source{：name'；~name：v'；~v})(var~name))。

然后，我们可以创建一个展开函数，该函数递归地将所有def符号替换为其对应的源代码：

(Defn Expand"；this采用类似于(chorge-numeral->；int(factorial-yc(int->；chetch-numeral 5)的形式，并展开所有函数定义，让我们直观地看到我们的lambda演算方法会是什么样子！"；[form](cond(Symbol？Form)(if-let[source(ome-&>；(str*ns*&34；/"；form)符号find-var meta：source)](展开(：v source))form)(序号？表单)(地图展开表单)：ELSE表单))

感谢Alex Reichert，Daniel Woelfel，Sean Grove，Irakli Safareli，Alex Kotliarskyi，Davit Magaltadze，Joe Averbukh审阅本文草稿