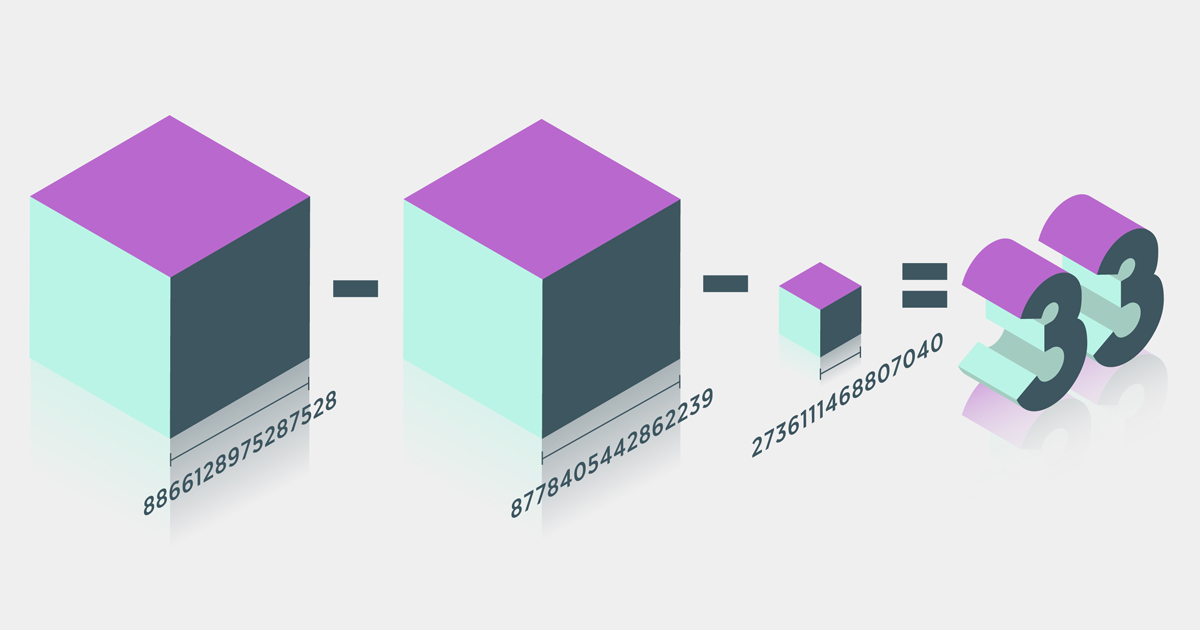
为“顽固”的33号解决了三个立方体之和的问题

数学家们长期以来一直在想，是否有可能将数字33表示为三个立方体的和-也就是说，方程33=x³+y³+z³是否有解。例如，他们知道29可以写成3³+1³+1³，而32不能表示为三个整数的和，每个整数的三次幂。但33人的案件64年来一直悬而未决。

现在，布里斯托尔大学(University Of Bristol)数学家安德鲁·布克(Andrew Booker)终于破解了这个问题：他发现(8,866,128,975,287,528)³+(-8,778,405,442,862,239)³+(-2,736,111,468,807,040)³=33。

布克通过设计一种新的搜索算法从千万亿种可能性中筛选出这三个奇怪的16位整数，从而发现了这三个奇特的16位整数。该算法在一台大学超级计算机上连续运行了三周。(他说，他认为这需要六个月的时间，但一个解决方案“出乎我的意料”。)。本月早些时候，当他的解决方案的消息传遍互联网时，其他数字理论家和数学爱好者们兴奋不已。根据一段关于这一发现的Numberphile视频，当布克发现这一发现时，他自己在办公室里欣喜若狂。

为什么这么兴高采烈呢？部分原因是找到这样一个解决方案的难度很大。自1955年以来，数学家们一直使用他们能用到的最强大的计算机来搜索满足“三个立方体之和”方程k=x³+y³+z³的三个整数的数字行，其中k是一个整数。有时解很容易，如k=29；有时，已知不存在解，如所有整数除以9后的余数为4或5，如数字32。

但通常情况下，解决方案是“不平凡的”。在这些情况下，三个立方整数-如(114,844,365)³+(110,902,301)³+(-142,254,840)³，等于26-看起来更像一张彩票，而不是任何具有可预测结构的东西。目前，数字理论家发现这种解决方案的唯一方法是一遍又一遍地玩数学“彩票”，利用计算机辅助搜索的蛮力，尝试不同的立方整数组合，并希望“中奖”。

但是，即使有越来越强大的计算机和更有效的算法来解决这个问题，一些整数仍然顽固地拒绝产生任何中奖彩票。33是一个特别顽固的例子：在布克找到他的解之前，它是仅有的两个低于100的整数之一(不包括那些肯定不存在解的整数)，它们仍然不能用三个立方体的和来表示。出了33个，只剩下42个了。[编者按：现在已经找到了42个。请参阅下面的更新。]。

花了这么长时间才找到33的解的原因是，在布克设计他的算法之前，在数字线上搜索足够远的地方-一直搜索到1016，或10万亿，然后同样向下搜索到负整数-在计算上是不切实际的，直到布克设计了他的算法。“与10年前的计算机相比，他不仅仅是在一台更大的计算机上运行这个东西--他找到了一种真正更有效的方法来定位解决方案，”奥地利科学与技术研究所(Institute Of Science And Technology)的数字理论家蒂姆·布朗宁(Tim Browning)说。

布克解释说，以前的算法“不知道它们在寻找什么”；它们可以高效地在给定的整数范围内搜索k=x³+y³+z³的任意整数k的解，但它们不能针对特定的整数，如k=33。他说，布克的算法可以，因此它的工作速度“在实际意义上可能快20倍”，比采取非目标方法的算法快20倍。