在一个伪造的模拟乘法器里

最近推特上一篇关于假冒模拟乘法器芯片的帖子吸引了我的注意，因为我既对假冒集成电路感兴趣，也对模拟计算机如何乘法感兴趣。在帖子中，约翰·麦克马斯特(John McMaster)拆解了一块可疑的AD633模拟乘法器芯片，发现里面有一个完全不同的罗克韦尔RC4200芯片。为什么会有人这么做？可能是因为RC4200(1978)目前的售价约为85美分，而更现代的激光修整1 AD633(1989)的售价约为7.2美元。

标有功能块的RC4200模拟乘法器管芯。照片由约翰·麦克马斯特提供。

模拟乘法有很多用途，如混频器、调制器和鉴相器，但我遇到的是模拟计算机。典型的模拟计算机使用电压来表示值，并通过插线板连接起来求解特定的方程。用运算放大器加或减两个值很容易，就像乘以一个常量一样。积分似乎很困难，但对于电容器来说几乎是微不足道的；模拟计算机擅长解微分方程。

然而，将两个值相乘出人意料地困难；相乘技术速度慢、不准确、噪音大或昂贵。一个精确但慢的乘法器使用的是旋转电位器的伺服电机的Rube-Goldberg配置。31969年的乘法器电路使用灯泡和光电池，一个快速而精确的方法是抛物线乘法器，它是由许多昂贵的高精度电阻器制成的。4我将要讨论的方法是把对数相加，然后取指数乘法。不方便的是，这种方法放大了晶体管之间的微小差异，而且对温度非常敏感，因此这种方法简单但不准确。

模拟器公司的240型模拟计算机。包括使用抛物线乘法器的模拟乘法器。

然而，模拟集成电路的发展为模拟乘法电路创造了新的机会，特别是由于集成电路中的晶体管是一起创造的，它们具有几乎相同的特性，并且微硅芯片上的元件都处于几乎相同的温度。5个。

我能找到的第一个模拟乘法器集成电路是1967年的电视解调器。吉尔伯特单元技术是由巴里·吉尔伯特在1968年提出的，现在大多数模拟乘法器中都使用吉尔伯特单元技术。6AD530是在1970年左右推出的，并成为行业标准，但需要外部调整以提高精度。在制造过程中，激光修剪集成电路内部的电阻大大提高了精度，这是AD633(被假冒的集成电路)中使用的一种方法。

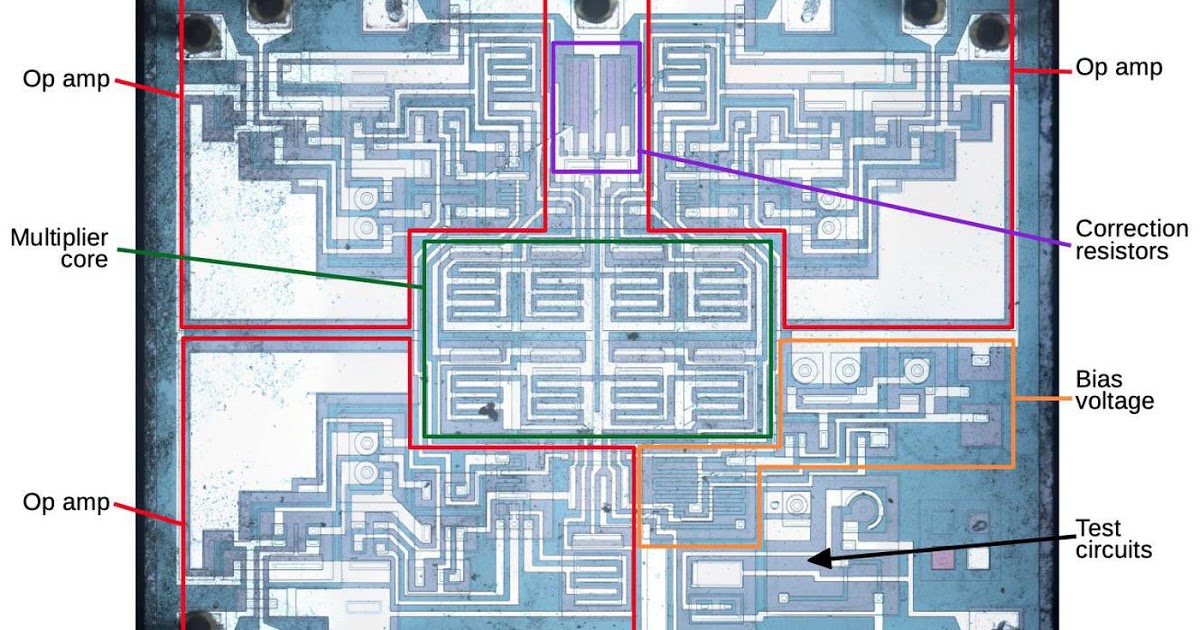
在解释RC4200(假冒芯片内的乘法器)的电路之前，我将先讨论一下构成它的元件，以及它们在集成电路中是如何出现的。这将帮助您识别芯片照片中的这些结构。

晶体管是芯片中的关键部件。下面的照片显示了RC4200中的一个NPN晶体管，因为它出现在芯片上。不同的蓝色是不同掺杂的硅区，形成N区和P区。白线是硅片顶部芯片的金属层，它们形成了连接到发射极(E)、基座(B)和集电极(C)的导线。

RC4200芯片上的NPN晶体管。发射器嵌入在底座中，集电极在下面。

您可能会认为PNP晶体管类似于NPN晶体管，只是交换了N和P硅的角色。但由于各种原因，PnP晶体管具有完全不同的结构。它们由圆形发射极(P)和环形基极(N)组成，环形基极(N)被集电极(P)包围。[4]与NPN晶体管的垂直结构不同，这形成了水平(横向)的P-N-P夹层。下图显示了RC4200中的一个PNP晶体管。

RC4200中的输入和输出晶体管比其他晶体管更大，并且具有不同的结构来支持更高的电流。下面的照片显示了其中一个输出晶体管。请注意发射器和底座的多个交叉指状手指。

电容器在运算放大器中非常重要，可以提供稳定性。集成电路中的电容器可以作为一块大金属板，由绝缘氧化层与硅隔开。IC上电容器的主要缺点是物理上非常大。RC4200中的15pF电容器的电容非常小，但却占据了芯片面积的很大一部分。在下面的照片中，红色箭头表示连接到电容器的金属层和电容器下面的硅层。

电阻器是模拟芯片的关键部件。不幸的是，IC中的电阻器非常不准确；不同芯片的电阻值可能相差50%。下面的照片显示了四个电阻器，它们使用不同的技术形成。第一个电阻器是左边的锯齿形蓝色区域。它是由一条P硅制成的，左右两边都有金属布线(白色)。它的电阻是3320Ω。右上角的电阻要短得多，所以只有511Ω(长的、窄的电阻器比短的、宽的电阻器有更高的电阻)。其余的电阻器都是小尺寸的，因为它们是夹点电阻器。在夹点电阻器中，顶部的方形棕色N硅层使导电区变得更薄(即夹点它)。对于给定的尺寸，这允许更高的电阻。(否则，20KΩ电阻器的长度将是第一个电阻器的6倍，占用过多的空间。)权衡的是夹点电阻器的精确度要低得多。

这种集成电路使用对数-反对数技术进行乘法运算。其思想是，如果你取两个数字的对数，将这两个数字相加，然后取反对数(即指数)，你就会得到这两个数字的乘积。通常，晶体管具有对数/指数特性：流过晶体管的电流是基极电压的指数。具体地说，如果Vbe是晶体管基极和发射极之间的电压，那么流过集电极的电流(IC)就是该电压的指数，如下图所示。模拟乘法器利用了这一特性。

这种方法的主要复杂性是上述曲线对温度和晶体管的制造特性非常敏感，由于曲线是指数型的，即使曲线的微小位移也会从根本上改变电流，这在用分立晶体管构建乘法器时是一个严重的困难，因为晶体管的特性随着晶体管的不同而不同。为了稳定温度，一些乘法器使用了温控炉子，但使用集成电路基本上解决了这些问题。集成电路中的晶体管是完全匹配的，因为它们是在相同条件下由同一片硅片制成的。而且集成电路管芯中的晶体管将处于几乎相同的温度。因此，集成电路使晶体管对数电路变得更加实用。

下图显示了RC4200乘法器芯片的结构。用户提供三个电流输入(I1、I2和I4)，芯片计算输出电流I3，其中I3=I1×I2？I4。(与使用电压的其他乘法器(如AD633)相比，使用电流输入和输出有点不方便。)。

数据手册中的RC4200乘法器的结构。请注意，电源电压(引脚3)为负。V OS1和V OS2是偏移量调整销，以提高精度。

图中的四个晶体管是乘法器核心，是IC运行的关键。晶体管的基极-发射极电压和：V BE3=V BE1+V BE2-V BE4。由于晶体管电流与电压呈指数关系，因此结果是I3=I1×I2？I4。

更详细地说，首先请注意，电压V BE1至V BE4通过晶体管控制集电极电流I C1至I C4(下图)。运算放大器调整基极-发射极电压，使输入电流与晶体管电流匹配，即I 1=I C1，依此类推。(这是通过运算放大器反馈实现的。)现在，如果您通过基极-发射极电压回路，从Q1的基极开始到Q4的基极(红色箭头)结束，您会发现V BE1+V BE2-V BE3-V BE4=0。(电压总和必须为零，因为您从接地开始，在接地结束。7)现在，由于iC与exp(Vbe)有关，取方程的指数得到iC1×iC2×iC3»iC4=1。(详细信息见脚注8。)。

接下来，我将解释V BE电压是如何产生的。每个电流输入都有一个与之相关联的运算放大器，该运算放大器使用反馈回路9为电流产生正确的VBE电压。例如，假设I_C太低，因此并非所有输入电流都流经晶体管。过多的电流将提高运算放大器负输入端上的电压，使其降低输出电压，从而降低晶体管的发射极电压。这会提高Vbe(因为基极现在将比发射极高)，导致更多的集电极电流流经晶体管。同样，如果流经晶体管的电流太多，运算放大器的输入将被拉低，从而降低Vbe。因此，反馈回路使运算放大器找到电流输入的准确Vbe。10个。

上面的电路工作得相当好，但是有一个复杂的问题：晶体管有一个很小的发射极电阻R。这个电阻上的电压降会使V_Be增加I_(CR)，扰乱指数行为。这就产生了非线性，降低了结果的准确性。数据手册上说，雷神公司已经开发出一种独特的、专有的方法来弥补这个不受欢迎的术语。他们没有进一步解释这一点，但通过研究骰子，我已经弄明白了它是如何工作的。

在补偿电路中，四个倍增晶体管中的每一个都与一个相同的镜像晶体管配对，并连接相应的发射器和相应的基极，如下所示。这些连接为成对的晶体管提供相同的基极和发射极电压，因此它们具有相同的集电极电流。换句话说，它们形成电流镜。镜像电流被馈入与不需要的发射极电阻相匹配的特殊校正电阻器中，根据数据手册，该电阻为0.1Ω。11校正电阻器两端的电压将与需要补偿的过电压相同(因为电阻和电流相同)。最后一步是将校正电阻器连接到乘法晶体管的基极，替换接地连接。这将按错误增加的量缩小V，从而修复计算。

主乘法器由四个晶体管组成。每个晶体管都有一个产生相同电流的镜像晶体管，用于校正发射极电阻。

为什么会有两个校正电阻器？回想一下，乘法器有两个晶体管加法和两个晶体管减法(即V BE1+V BE2-V BE3-V BE4=0)。为了处理这一问题，将校正电路一分为二。左半部分将I C1和I C2相加，并将该电流施加到Q3/Q4侧的校正电阻器，而右半部分将I C3和I C4相加，并将其施加到Q1/Q2侧的校正电阻器。加减运算得出所需的净校正。

下面的原理图显示了RC4200的完整电路，我突出显示了主要功能模块。(不便的是，直到我从芯片照片中找出电路后，我才找到这个原理图。)上面讨论了乘法器内核和校正电阻器。运算放大器电路与我写过的741运算放大器非常相似。它们缺少典型运算放大器的输出级；输出晶体管(Q112/Q212/Q412)对应于典型运算放大器的中间增益状态。偏置电路(橙色，右下角)为运算放大器提供固定的偏置电压。12个。

在集成电路出现之前，模拟乘法是很难实现的。然而，集成电路使得制造匹配的晶体管变得容易，导致了快速、廉价的模拟乘法集成电路。不幸的是，模拟乘法器集成电路的引入正值模拟计算机的消亡，被廉价的数字微处理器所扼杀，因此模拟计算错过了这些芯片的大部分好处。

虽然大多数模拟乘法器使用称为吉尔伯特单元的电路，但雷神RC4200模拟乘法器使用不同的技术来乘除由电流表示的值。虽然它包括一个特殊的误差补偿电路来提高其精度，但与精确的激光修剪乘法器相比，它已经过时了。现在，造假者重新贴上RC4200芯片的标签，并将其作为更昂贵的AD633乘法器出售。

我在推特上宣布了我最新的博客帖子，所以请关注kensheriff上的最新消息。我还有一个RSS提要。感谢约翰·麦克马斯特在这篇博客中使用的芯片照片；照片在这里。

AD633乘法器如此昂贵的原因之一是，芯片上的电阻器是激光修整的电阻器，以保证精度。为了获得准确的结果，模拟乘法器需要精确调谐的电阻。老款的RC4200型需要可调的外部电阻器，这就不太方便了。--↩。

我对这种假冒芯片感到有点困惑。有时人们会把便宜的运算放大器贴上昂贵的运算放大器的标签，正如齐普托巴解释的那样。乍一看，这就是这里正在发生的事情：廉价的乘法器被重新包装成昂贵的乘法器。但是，这两个多路转换器是如此不同，以至于我可以。I don‘我根本无法想象其中一个会取代另一个。具体地说，AD633接受差动电压输入并输出两个电流(差动电流)，它计算A×B+C。另一方面，RC4200接受电流输入，输出单个电流，它计算A×B&A；divC。↩。

伺服倍增器的一个例子是20世纪50年代末的Solartron伺服倍增器。这个17磅的单元包含一个由伺服电机控制的电位器，允许它将+/-100伏表示的数字相乘。考虑到它的机械操作，它的速度惊人地快，响应时间不到30毫秒。耗电量很高：70瓦，由风扇冷却。(相比之下，RC4200芯片的功耗为40毫瓦。)

↩这张照片显示的是SolartronTJ961型伺服旋转变压器。这实现了乘法和正弦/余弦计算。来自模拟博物馆手册的照片。

1969年的模拟计算机I&#m RESTORY使用抛物线乘法器，这是一种用于高精度乘法的技术。其思想是为了计算A×B，计算具有相同值的((A+B)&；Hat2-(A-B)&；Hat2)/4。该方程看起来比原来的乘积复杂得多，但在模拟计算机上实现起来更容易，因为运算放大器可以执行加、减和除以4的运算。(A+B)&；Hat2-(A-B)&；Hat2)/4。平方比乘法容易，因为它是单变量的函数，所以它可以由任意函数生成器实现。

上面的照片显示了一块来自模拟计算机的功能板，用于计算平方，即抛物线。该板由多个分段线性段近似函数，每个分段线性段由电阻器定义。(请注意左侧极为精确的0.01%电阻器。)中间的金属块容纳二极管，由金属进行温度平衡。每个二极管都偏置为在特定电压下导通；二极管充当开关，为每个线性段选择合适的电阻。请注意乘法所需的大量精密硬件；单个产品需要两个抛物线功能板和多路放大器。-↩。

为了将温度对集成电路的影响降到最低，关键的乘法器晶体管被紧密地放置在芯片的中心，如果芯片两端存在温度梯度，这将使晶体管之间的温差降到最小。(例如，与将晶体管放在角落相比。)为了进一步降低温度梯度，数据手册指定了一条热对称线。在这条线路上放置一个温度源可以确保温度较高的晶体管相互抵消。

吉尔伯特单元的发明者巴里·吉尔伯特有一段视频解释了跨线性电路，即基于双极晶体管的指数电流-电压关系的电路。这个视频详细解释了跨线性模拟乘法器，讨论了两种方法>；第一种方法是对数反对数法，由运算放大器强制并感测集电极电流。第二种方法是集成方法，由电压到电流转换、差分电流模式内核和电流到电压转换构建而成。(↩)。

值得一提的是，该芯片使用-15V电源，因此接地是最高电压，其他内部电压均为负。这只是一个警告，因为与接地是低电压的电路相比，这会使事情变得混乱和倒退。-↩。

基极电压和集电极电流之间的关系由Ebers-Moll模型给出。下面的方程充满了有趣的常数：α：a增益因子(几乎为1)，k：玻尔兹曼常数，IS：饱和电流(非常小，数量级为10-15A)，T：绝对温度，Q：电子上的电荷。(指数项中的温度反映了温度稳定性对乘法器的重要性。)。

用热电压VT(约26 mV)代替KT/Q，进行一些较小的近似，并取对数收益率：

取指数并假设所有晶体管都具有相同的温度和饱和电流，则产生与四个电流相关的所需方程：

这个方程式显示了四个电流是如何通过乘法和除法联系在一起的。更多详细信息，请参阅数据手册。-↩。

从某种意义上说，运算放大器计算晶体管的指数函数的逆函数。晶体管以Vbe为输入，产生指数电流作为输出。然而，我们有电流作为输入，想要对数电压作为输出。通过在其反馈回路中使用带函数的运算放大器，我们可以找到函数的逆函数，在这种情况下给出对数。也就是说，运算放大器将收敛于输出X，其中f(X)等于输入，即X=f-1<；，在这种情况下，运算放大器将收敛于输出X，其中f(X)等于输入，也就是X=f-1<；在这种情况下，运算放大器将收敛于输出X，其中f(X)等于输入，即X=f-1<；/sup(输入)。可以使用相同的技术从乘法器芯片生成平方根：使用乘法器对其输入平方，然后使用运算放大器计算反函数，即平方根。-↩。

你可能会想，为什么运算放大器找到了正确的值，却没有超调和振荡。抛开所有的理论不谈，我们的想法是运算放大器输入端的电容器可以稳定它，防止振荡。即便如此，数据手册也警告说，当输入电流接近0时，电路会变得不稳定。这相当于被零除，所以电路处理得不好也就不足为奇了。从数学上讲，运算放大器正在试图找到ln(0)，而ln(0)不是ln(0；)，这与被零除相对应。从数学上讲，运算放大器正在试图找到ln(0)，而ln(0)不是ln(0；)，这相当于除以零。从数学上讲，运算放大器正在试图找到ln(0)，而不是ln(0)，而不是ln(0)。如果你想乘以零或负值，数据手册描述了如何用电阻器对输入进行偏置，以保持输入为正，但仍能得到正确的答案。-↩。

下面的两个电阻器用于发射极校正；它们具有不同寻常的结构和非常。

.