最终失败的模式

是小于或等于素数的一个很好的近似值，数字证据表明它总是大于例如，

这就提出了一个问题：第一次超过的时间是什么时候？1933年，利特尔伍德的学生Skewes证明，假设黎曼假设，它必须在一些小于或等于。

后来，在1955年，Skewes证明了在没有Riemann假设的情况下，对于一些小于。

到目前为止，这个界限已经有了很大的改善。我们现在知道这两个函数在附近的某个地方交叉，但我们不知道这是否是第一个交叉！

这是个不错的图案。但这种模式不会永远持续下去！它会持续很长很长一段时间…。但不是永远。

但不是所有人都会在某个时候停止工作，再也不会工作了。事实上，这对所有人来说都是绝对失败的。

直到我读到格雷格·伊根根据汉斯佩特·施密德的作品所作的解释，我才明白这一点。这一切都是关于卷积和傅立叶变换：

假设我们有一个矩形脉冲，以原点为中心，高度为1/2，半宽为1。

现在，假设我们一遍又一遍地计算这个函数的移动平均值，平均值是在半宽1/3的窗口中计算的，然后是1/5，然后是1/7，1/9，依此类推。

在这个过程的最初几个阶段，原始脉冲的几个特征将完全保持不变，但随后它们将在某个时间点突然消失。

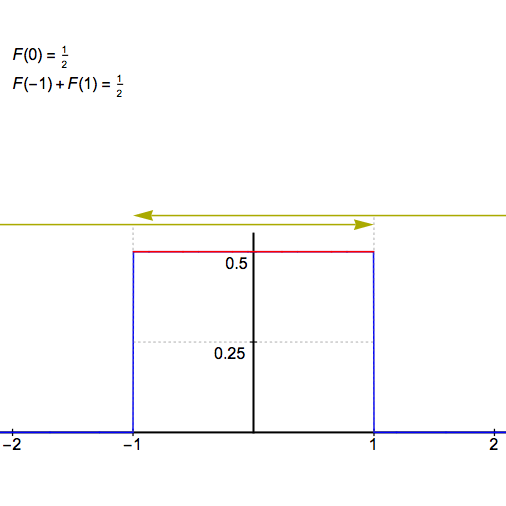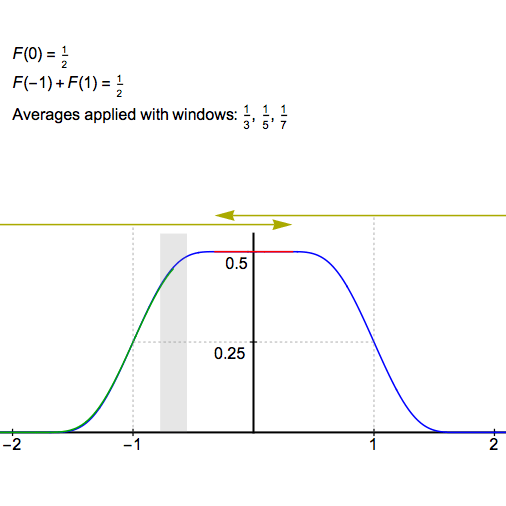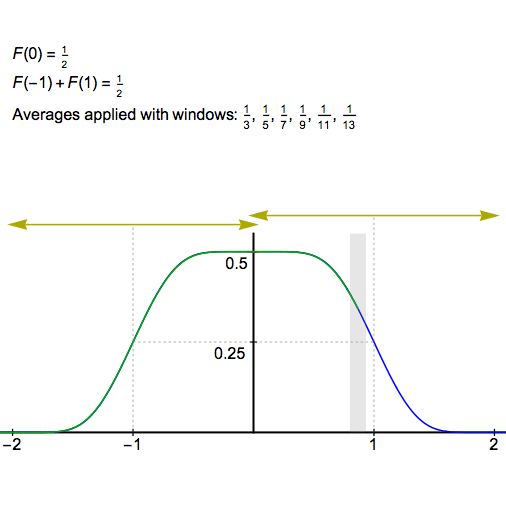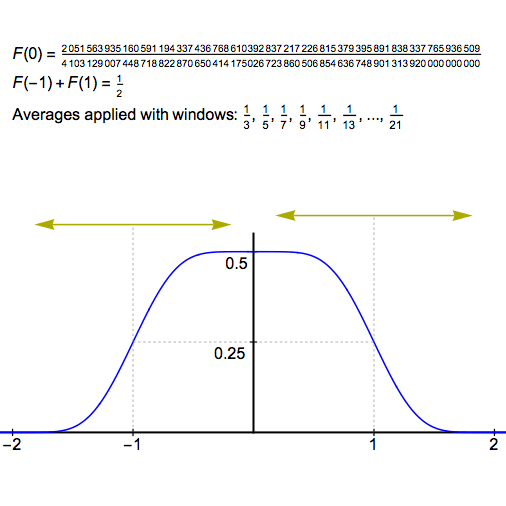
第一个特征是F(0)=1/2。在原始脉冲中，点(0，1/2)位于平台上，这是一个完全恒定的段，半宽为1。重复取移动平均值的过程将蚕食这个平台，将其半宽缩小平均窗口的半宽。因此，一旦窗口的半宽之和超过1，则在1/3+1/5+1/7+…。+1/15，F(0)会突然降到1/2以下，但在此步骤之前，F(0)将保持不变。

第二个特征是F(-1)=F(1)=1/4。在原始脉冲中，我们在-1和1处有一个步长，但是如果我们在这里将F定义为左手和右手极限的平均值，我们得到1/4，一旦我们应用第一个移动平均数，我们就有1/4作为函数值。

在这种情况下，只要点(-1，1/4)和(1，1/4)被函数具有适当对称性的区域包围，F(-1)=F(1)=1/4将继续成立：它等于一个奇函数，从原点偏移并平移到这些中心。只要这对于比平均窗口更宽的区域是正确的，那么中心的平均值就不会改变。

每个对称斜坡的初始半宽为2(从高原的另一端延伸，沿x轴的距离相等)，与高原一样，每次我们再取一条移动平均线时，它都会被蚕食掉。在这种情况下，要素将持续到1/3+1/5+1/7+…。+1/113，即总和首次超过2时。

∫sin(T)/tdt=π/2∫sin(t/3)/(t/3)×sin(T)/tdt=π/2∫sin(t/5)/(t/5)×sin(t/3)/(t/3)×sin(T)/tdt=π/2。

这里这些积分是从t=0到t=∞。施密德想出了一个他自己更持久的模式：

∫2 cos(T)sin(T)/t dt=π/2∫2 cos(T)sin(t/3)/(t/3)×sin(T)/t dt=π/2∫2 cos(T)sin(t/5)/(t/5)×sin(t/3)/(t/3)×sin(T)/t dt=π/2…。∫2 cos(T)sin(t/111)/(t/111)×…。×sin(t/3)/(t/3)×sin(T)/tdt=π/2。

由于Borwein，第一组积分对应于对我们的更平滑的脉冲序列进行傅立叶变换，然后计算F(0)。Sinc函数的傅里叶变换：

与半宽w的矩形脉冲成正比，并且sinc函数乘积的傅立叶变换是它们的变换的卷积，在矩形脉冲的情况下，这正好等于取移动平均值。

施密德积分来自于增加了一个巧妙的扭曲：2cos(T)的额外因子将积分从零频率傅立叶分量移到角频率为-1和1的分量之和，因此结果取决于F(-1)+F(1)=1/2，正如我们已经看到的，这种情况持续的时间比F(0)=1/2长得多。

·汉斯佩特·施密德(Hanspeter Schmid)，两个奇怪的积分和一个图形证明，埃莱姆。数学课。69(2014)11-17。

我问格雷格，我们是否可以推广这些结果，给出最终失败的更长的恒等式序列，他向我展示了如何：你可以只取博尔文积分，并将数字1，1/3，1/5，1/7，…替换为1，1/3，1/5，1/7，乘以某个正数序列。

那么只要它超过1就等于了，但当它超过1的时候就不一样了。你可以在维基百科上看到完整的解释：

只需做一点工作，就可以使这些估计值大大提高，尽管还需要更多的工作才能找到其中的确切价值。