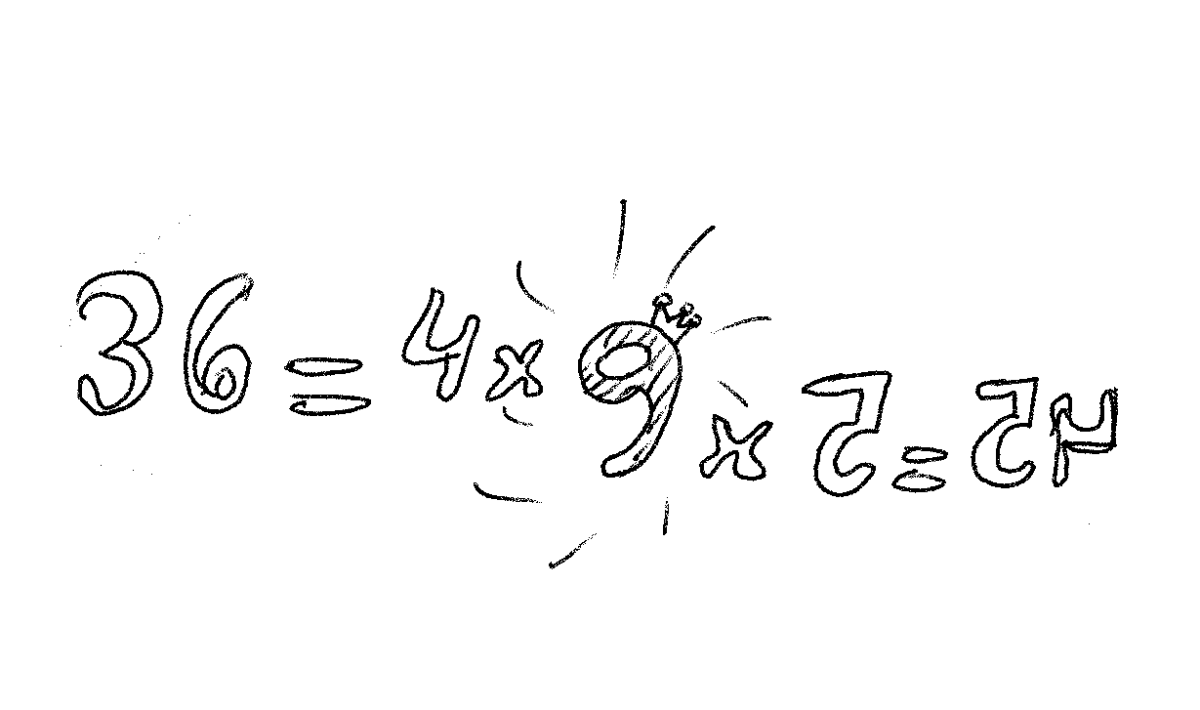GCD与减法的魔力

最大的公约数是我在学校里学到的，但它是那种“那又怎么样？”研究对象。但是最近我又去了一次，它非常有趣。

每个数，都可以表示为素数的乘积。每个数字的这个产品都是独一无二的；就像是说，每个数字都有一个指纹。这就是所谓的算术基本定理。36是4x9，45是5x9。这意味着一些数字将具有彼此的共同部分。

这些公共部分可以将这两个数相除，因此它们是公约数。在上面的示例中，36是4x9或2x2x3x3，而45是5x3x3；3是两者的公约数，3x3也是9；但9是36和45的最大除数。

我年轻的时候有一个问题，那就是为什么我们谈论的是“最伟大的”而不是最小的公约数。我们可以，但是很快，这就变得无聊了：每个数的最小公约数是1，然后在1和gcd之间有一些公约数。但GCD的独特之处在于，它接受两个数字，并给出两个数字的所有公共部分。

这太酷了！不寻常的部分是相对质数的！-意思是，它们除了数字1之外没有什么共同之处。

因此，要找到GCD，我们需要找到这两个数字在写成素因数时的所有公共部分。

36=3x3x2x2和45=3x3x5，因此36和45的GCD是3x3，即9。因此36是9(4)，45是9(5)。将数字视为GCDS的倍数是非常有趣的。此外，请注意，上例中的这些乘数4和5是相对质数。

减去两个相对质数，将得到另一个数字，虽然它本身不一定是质数，但相对于前面的两个数字都是相对质数。举个例子，13-7=6.6不是素数，但它对7和13都是相对的素数，如果我们从13中减去6，我们又会得到7，这不是很有趣。但如果我们从较小的7减去6，因为6和7是相对质数，我们应该得到另一个对它们都是相对质数的数字；如果继续这样做，7-6=1，它对每一个其他数字都是相对质数的：